Astronomía Zetética (S. Rowbotham) Capítulo XIV: El Gran círculo

Capítulo XIV: Examen de las llamadas "pruebas" de la esfericidad terrestre Navegación De Gran Círculo Entre la gente e la tierra, prevalece una gran cantidad de ideas erróneas sobre lo que realmente significa la llamada "navegación de gran círculo"; y, a pesar de que el tema se entiende de manera imperfecta, el "proyecto" o hipótesis, (porque no es nada mas que eso), a menudo se toma muy apresuradamente como una prueba adicional de la esfericidad de la Tierra. Pero, como todas las demás "pruebas" que se han dado, no hay una conexión necesaria entre los hechos aducidos y la teoría que se pretende probar. Aunque los navegantes profesionales están familiarizados con varios modos de navegación: "navegación paralela", "navegación en plano", "navegación en travesía", "navegación en curso", "navegación en latitud media", "navegación en Mercator" y "navegación de gran círculo" Los métodos "Mercator" y "Gran círculo" son ahora los favoritos. Casi todos los sistemas anteriores requerían la navegación por, o en relación con Líneas de trazos, o líneas en ángulo recto a las líneas del meridiano; y si la Tierra es plana o un Globo, estos no están geométricamente en ángulos rectos a las líneas de latitud, excepto en el ecuador. Por lo tanto, la proyección de Mercator, debido a que sus líneas de latitud y longitud son cuadradas entre sí, ha sido empleada casi universalmente. Pero antes de la adopción general del plan de Mercator, muchos navegantes destacados vieron que las Líneas de trazos navegando sobre un globo, era prácticamente una serie de pequeños círculos, y concebían un método muy similar al que ahora se llama el sistema del "gran círculo". Ya en 1495, Sebastian Cabot sugirió la adopción de este método. También fue defendido en 1537 por Numez, y en 1561, y posteriormente por Cortés, Zamarano y otros. Después de permanecer inactivo durante mucho tiempo, el sistema fue reavivado por el Sr. Towson, de Devonport, quien leyó un artículo ante la Society of Arts, en mayo de 1850, y luego presentó sus "tablas para facilitar la práctica de la navegación en círculos". "a los señores Comisionados del Almirantazgo, quienes" ordenaron que se imprimieran para el uso de todos los marineros ". Muchas personas suponen que las palabras "navegación de gran circulo", simplemente significan que el marinero, en lugar de navegar en línea directa de un lugar a otro, en la misma latitud, toma un camino indirecto hacia el sur o el norte de esta línea directa, donde siendo los grados de longitud más pequeños, la distancia pasada, aunque aparentemente mayor, en realidad es menor. Luego se argumenta falsamente que como "la mayor distancia de recorrido, es el camino más cercano", los grados de longitud deben ser más pequeños y, por lo tanto, la Tierra debe ser un globo terráqueo. Este es otro ejemplo del auto-engaño practicado por muchos de los defensores de la esfericidad. Es realmente doloroso reflexionar sobre la manera en que una hipótesis meramente fantasiosa, ha reducido a sus defensores a la prostitución mental. Es una pobre criatura perdida, que vagamente busca algo, o todo lo que satisfaga sus anhelos, es solo un tipo de vagabundo filosófico, que busca y busca lo que sea que pruebe, o que solo parezca probar su única idea. Su incontrolable anhelo de algo, para confirmar sus nociones, y satisfacer su deseo de ser sabio y grande. El motivo que impulsa a un mayor número de filósofos modernos, no puede ser menor u otro que el amor a la distinción. Si fuera un amor a la verdad, al progreso humano, y al bienestar, examinarían escrupulosamente las premisas sobre las cuales se basan sus teorías. Pero esto, los defensores de la esfericidad y el movimiento de la Tierra, rara vez o nunca lo han hecho. No hay una sola instancia registrada donde incluso se admite la necesidad de hacerlo. De ahí que si bien está prohibido cuestionar las bases, se aprovechan abruptamente de todo lo que ¨da color¨ a sus suposiciones, aunque en muchos casos no son pertinentes, ni lógicamente consistentes. En el caso que tenemos ante nosotros, la contracción o convergencia de los grados de longitud más allá del ecuador no está probada; y nuevamente, si fueran convergentes, no podría haber una pulgada de ganancia en tomar el llamado curso de gran círculo entre dos lugares al este y al oeste entre sí. Que se pruebe el siguiente experimento, como prueba de esta afirmación. En un globo artificial, marque un gran camino circular, entre Ciudad del Cabo y Sydney, o Valparaíso y Ciudad del Cabo. Tome una tira de lámina de plomo, y dóblela a la forma de este camino; y después de hacerlo recto, mida su longitud en comparación con el paralelo de latitud entre los lugares. El resultado satisfará completamente al experimentador de que esta visión de la navegación en gran círculo, es contraria a los principios geométricos conocidos. Estrictamente hablando, no es en absoluto la "navegación de gran circulo" lo que el Sr. Towson, y los Señores del Almirantazgo, han recomendado. Las palabras ¨gran círculo¨, solo se usan en comparación con los círculos pequeños que se describen en la navegación en  vías de rumbos lineales. "El principio fundamental de este método es el axioma de la geometría esférica, que la distancia más corta entre dos puntos en la superficie de una esfera, se encuentra en la línea de un gran círculo o, en otras palabras, de un círculo que pasa por el centro. de una esfera. Pero los mapas y las gráficas, que son representaciones planas de la superficie de un globo, están necesariamente distorsionadas, y solo son correctas cerca del ecuador, la distorsión aumenta a medida que se acercan los polos; El globo terráqueo es el más corto, está en el gráfico hecho para parecer mucho más largo y al revés. Esto se demostró claramente en la comparación en un gráfico y en un globo del curso entre Van Dieman's Land y Valdivia. en la costa occidental de América del Sur: el curso, que según el gráfico parecía ser una línea recta, cuando se colocaba sobre el globo terráqueo se encontró muy indirecto, mientras que la línea de Gran círculo, cortando los dos puntos, apareció en la tabla como un bucle de gran longitud." "Mercator y la navegación paralela conducen la nave por una ruta indirecta en comparación con la vía de Gran círculo". En el lenguaje náutico, la navegación en rumbos lineales, que se practicó casi universalmente antes de la reciente introducción de la navegación de Gran círculo, consiste en seguir paralelos en ángulo recto a las líneas meridianas, y como se supone que estas líneas meridianas son convergentes, es evidente que el rumbo de un barco navegado de esa forma, no es el más directo; una gran trayectoria circular es una en ángulos menores a 90° al norte y al sur del meridiano. Si el lector dibuja una serie de líneas de trazo en un mapa del "globo terráqueo", enseguida verá que el curso es indirecto. Pero si dibuja líneas con un ligero ángulo hacia el norte (en el norte), y hacia el sur (en la región sur) hacia las líneas de rumbo mencionadas anteriormente, pronto notará que el rumbo del barco es más directo, y por lo tanto, el marinero en vez de adoptar el llamado método de "Gran círculo", ahorrará tiempo y distancia, pero solo en comparación con la ruta de la línea de rumbo. Este método de ¨Gran círculo¨ no es absolutamente la ruta más corta, ya que la Tierra es plana, los grados de longitud en el sur debe divergir o expandirse, y extenderse a medida que aumenta la latitud, y los paralelos o líneas de latitud deben ser círculos concéntricos con el centro norte. Por lo tanto, en realidad hay un camino aún más corto que la vía de la línea de rumbo, o el curso del ¨Gran círculo¨. Esto será evidente al intentar el siguiente simple experimento. Coloque una luz, para representar el sol, a una altura de por ejemplo, dos pies en el centro de una mesa redonda. Dibuja líneas desde el centro a la circunferencia para representar líneas meridianas. Marque dos lugares para representar Ciudad del Cabo y Melbourne; ahora tome cualquier objeto pequeño que represente a un barco que navega de uno de estos lugares al otro,al moverlo hacia adelante, manteniendo la luz a la misma altitud durante todo el recorrido se verá la línea de latitud o trayectoria de la nave como un arco de círculo, que prácticamente es una ruta de Gran círculo, mientras que la línea de rumbo y la ruta mayor, se representarían mediante una serie de tangentes a las líneas meridianas entre los dos lugares. La ruta más cercana posible geométricamente es la cuerda (geometría) o línea recta que une los extremos del arco que forma la línea de latitud. Que se dibuje esta línea o cuerda (geometría), y dejemos que todos los argumentos sean superfluos ... la proposición será inmediatamente evidente por sí misma. Por lo tanto, hemos visto que la navegación de Gran círculo, no es la ruta más corta posible, sino simplemente más corta que otras rutas que en teoría se han sugerido y adoptado; y afirmar que los resultados son confirmatorios o demostrativos sobre la esfericidad de la Tierra, es en el más alto grado ... ilógico.

No es el propósito de este blog explicar en profundidad qué es el gran círculo. Una simple búsqueda en Google le ofrecerá múltiples enlaces en donde ampliar el concepto.  Lo importante para el tratamiento de este título del libro de Rowbotham es saber que el Gran Círculo, denominado también círculo mayor o círculo máximo, es el círculo resultante de una sección realizada a una esfera mediante un plano que pase por su centro y la divida en dos hemisferios; la sección circular obtenida tiene el mismo diámetro que la esfera y que la distancia más corta entre dos puntos de la superficie de una esfera siempre es el arco de círculo máximo que los une.

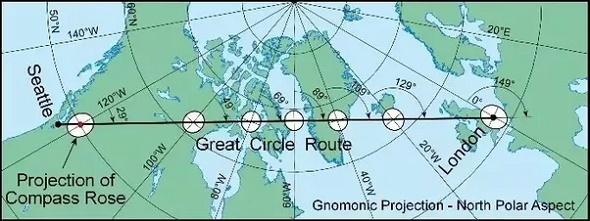
Veamos este caso: Consideremos la ruta Seattle-Londres. Vista sobre una proyección de Mercator las rutas loxodrómica (línea de rumbo) y ortodrómica (gran círculo). La primera corta todos los meridianos y paralelos en el mismo ángulo, el rumbo es 087 desde la salida hasta la llegada. A simple vista parece la opción más razonable, mientras que la  segunda transcurre a lo largo de una gran curva que se dirige hacia el noreste al principio y constantemente va variando de rumbo hasta terminar dirigiéndose hacia el sureste. Parece mucho más larga, cierto?

Sin embargo, si utilizamos un mapa de la Tierra Plana, la ruta ortodrómica parece cobrar sentido. Ahora resulta ser el camino más corto, mientras la línea de rumbo es la que recorre el camino más largo: 

En la siguiente imagen, podemos ver la misma ruta sobre la esfera:

Y ahora, veamos el mismo camino en Google Maps y comparémosla con la primer imagen. Como puede apreciarse, en ambos casos tenemos la misma ruta

ignifica esto que el mapa de la Tierra plana es el correcto entonces? La respuesta es un gran "NO". Si bien en este caso en particular se aproxima bastante, ya que estamos considerando una ruta cercana a su centro, la cosa cambia mucho cuando nos alejamos de él. Veamos la ruta propuesta para Ciudad del Cabo hasta Melbourne por Rowbotham en su curioso experimento.

El camino nos llevaría desde Ciudad del Cabo hacia el norte, cruzando la mayor parte del continente africano, atravesaría el Mar Rojo, el norte de India, el norte de Vietnam y atravesaría finalmente Australia desde el noroeste hacia el sureste.

En la siguiente imagen, podemos ver esta misma ruta en color verde y la de gran círculo en negro (aproximándose a la Antártida). Obviamente en este caso ya no coinciden como en el primer caso. También podemos ver la línea de rumbo marcada en rojo

Y cómo se vería esta ruta de gran círculo sobre la esfera? Veamos...

Esta ruta, de poco más de 10.300 km, es la que se utiliza en realidad. El gran círculo SIEMPRE es la distancia más corta, tal cosa solo es posible en una esfera.

Anterior: Capítulo XIV:  Estaciones y distancias
Siguiente: Capítulo XIV: Movimiento de las estrellas en el norte y en el sur