Astronomía Zetética (S. Rowbotham) Capítulo V

Capítulo V: La verdadera distancia del sol Ahora se demuestra que la tierra es un plano, y por lo tanto la distancia del sol puede ser fácilmente y con mayor precisión determinada por el proceso más simple posible. La operación es una en trigonometría plana, la cual no admite incertidumbre y no requiere modificación o tolerancia para influencias probables. El principio implicado en el proceso puede ilustrarse mediante el siguiente diagrama, la fig. 56. Fig. 56 Sea A un objeto, cuya distancia se desea, en el lado opuesto de un río. Colocar una varilla verticalmente en el punto C, y tomar un pedazo de cartón fuerte, en forma de triángulo rectángulo, como B-C-D. Es evidente que la colocación de la Mirando a lo largo del lado D-B, la línea de visión D-B-H, pasará a la izquierda del objeto A. Al mover el triángulo más a la derecha, a la posición E, La línea E-F, seguirá pasando a la izquierda de A; Pero al desplazarlo nuevamente a la derecha, hasta que la línea de visión de L coincida con el objeto A, se verá que L-A, lleva la misma relación con A-C-L, como D-B lo hace a B-C-D: en otras palabras, los dos lados del triángulo B-C y C-D, son iguales en longitud, por lo que las dos líneas C-A y C-L son iguales. Por lo tanto, si se mide la distancia de L a C, será en realidad la misma que la distancia deseada de C a A. Será obvio que el mismo proceso aplicado verticalmente es igualmente cierto en sus resultados. En una ocasión, en el año 1856, El autor habiendo impartido anteriormente un curso de conferencias en Great Yarmouth, Norfolk, y este tema se volvió muy interesante para algunos de sus auditores, se le invitó a encontrarse en la orilla del mar; Y entre otras observaciones y experimentos, para medir, por el proceso anterior, la altura del Monumento de Nelson, que se encuentra en la playa cerca del mar. Un pedazo de cartón grueso se cortó en forma de un triángulo rectángulo, la longitud de los dos lados es de unos 8 pulgadas. Un fino hilo de seda, con un guijarro unido, constituía una plomada, fijada con un alfiler a un lado del triángulo, como se muestra en P. El propósito de esta plomada era permitir al observador mantener el triángulo en una posición verdaderamente vertical. Al mirar sobre el triángulo sostenido verticalmente, y un lado paralelo con la plomada P, desde la posición A, La línea de visión cayó sobre el punto B; Pero al caminar gradualmente hacia atrás, la parte superior del casco D, sobre la cabeza de la figura de Britannia, que sobrepasa la columna, fue finalmente visible desde el punto C. Al prolongar la línea D,-C hasta H, por medio de un vástago, se midió la distancia desde H al centro del Monumento en O, y resultó que la altitud O-D era igual a O-H Fig. 57 Posteriormente la altitud se obtuvo a partir de un trabajo publicado en Yarmouth, y se encontró que difieren sólo una pulgada de la altitud determinada por la simple operación descrita anteriormente. Las observaciones e ilustraciones anteriores no son, por supuesto, necesarias para el matemático; Pero puede ser útil al lector general, mostrándole que la trigonometría plana, llevada a cabo sobre el plano o superficie horizontal de la tierra, permite operaciones simples y perfectas en principio, y en la práctica plenamente confiables y satisfactorias. Las ilustraciones dadas arriba se refieren a un objeto fijo; Pero el sol no es fijo; Por lo tanto, debe adoptarse una modificación del proceso, pero con el mismo principio. En lugar del simple triángulo y la plomada, representados en la Fig. 57, debe emplearse un instrumento de arco graduado, y dos observadores, uno en cada extremo de una línea de base norte y sur, deben observar al mismo tiempo el borde inferior del sol al pasar por el meridiano; Cuando, a partir de la diferencia en el ángulo observado, y la longitud conocida de la línea de base, se puede calcular la distancia real del sol. El siguiente caso ilustrará plenamente esta operación, así como sus resultados e importancia: La distancia desde el puente de Londres a la costa del mar en Brighton, en línea recta, es de 50 millas terrestres (80 km). En un día determinado, a las 12 horas, se encontró que la altitud del sol, cercana al agua en el puente de Londres, era de 61 grados de arco; Y en el mismo momento se observó que la altitud desde la costa del mar en Brighton era de 64 grados de arco, como se muestra en la Fig. 58. La línea de base de L a B, es de 50 millas terrestres; El ángulo en L, 61 grados; Y el ángulo en B, 64 grados. Además del método por cálculo, la distancia del borde inferior del sol puede ser determinada a partir de estos elementos por el método llamado "construcción". El diagrama, fig. 58 , es el caso anterior "construido"; Es decir, la línea de base de L a B representa 50 millas terrestres; y la línea L-S Se dibuja con un ángulo de 61 grados, y la línea B-S, con un ángulo de 64 grados. Ambas líneas se prolongan hasta que se cruzan en el punto S. Luego, con un par de compases, mida la longitud de la línea de base B-L y vea cuántas veces puede encontrarse la misma longitud en la línea L-S o B-S. Fig.58 Se encontrará que es dieciséis veces 50 millas, igual a 800 millas terrestres (1287 km). Luego mida de la misma manera la línea vertical D-S, y se verá que es de 700 millas (1126 km). Por lo tanto es demostrable que la distancia del sol sobre esa parte de la tierra a la cual es vertical es solamente 700 millas terrestres. Por el mismo modo se puede comprobar que la distancia desde Londres de esa parte de la tierra donde el sol era vertical en el momento (13 de julio de 1870) las observaciones anteriores fueron tomadas, era sólo 400 millas terrestres (643 km), como se muestra dividiendo el Línea de base L-D, por la distancia B-L. Si se quiere tener en cuenta la refracción -que sin duda existe cuando los rayos del sol tienen que pasar a través de un medio -la atmósfera, que aumenta gradualmente en densidad A medida que se aproxima a la superficie de la tierra- disminuirá considerablemente la distancia antes mencionada del sol; El método anterior de medir distancias se aplica igualmente a la luna ya las estrellas; y es fácil demostrarlo, colocarlo más allá de la posibilidad de error, mientras se excluyen premisas supuestas, que la luna está más cerca de la tierra que el sol, y que todas las luminarias visibles en el firmamento están contenidas dentro de una distancia vertical de 1000 millas terrestres (1609 km); de lo cual se deduce inevitablemente que la magnitud del sol, de la luna, de las estrellas y de los cometas es comparativamente pequeña - mucho más pequeña que la tierra de la cual se miden, y a la cual, por lo tanto, deben necesariamente ser secundarias. Y subserviente. En realidad, no pueden ser nada más que "centros de acción", arrojando luz y productos químicos sobre la tierra.

Ya desde el inicio afirma Rowbotham que la planitud de la tierra está demostrada, por lo que no toma en cuenta la curvatura terrestre al hacer las observaciones.

Tomando como referencia la línea Londres Brighton hace sus cálculos:

Determina la altura del sol en Londres en 64º y en 61º para Brighton. Con esos datos, calcula que la vertical del sol se encuentra a 400 millas (643 km) al sur de Londres a una altitud de 700 millas (1126 km). Veamos entonces dónde estaba el sol el 13 de julio de 1870

Resulta entonces que el sol se encontraba justo encima de la localidad de Foussignac, en Francia, la que está sobre la latitud 45°42′N.

Esto deja al sol fuera de los límites impuestos por los trópicos. Esto ya es suficiente para concluir que hay un error muy grave en el cálculo que ha realizado. Por la fecha (13 de julio) sabemos que el sol debería hallarse aproximadamente en el primer tercio de su recorrido entre el Trópico de Cáncer y el ecuador, a varios miles de kilómetros de la ubicación estimada por Rowbotham.

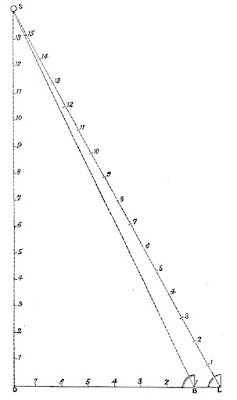
Además, la diferencia entre la latitud de Foussignac y la de Buenos aires es de 80.3 grados, lo que equivale a 5545 millas o 8923 km. Otras ciudades como Montevideo o Ciudad del Cabo están ubicadas en latitudes similares. Si el cálculo de Rowbotham estuviera acertado, el mediodía de mediados de julio en esas latitudes nos mostraría al sol apenas 7º por sobre el horizonte, según se puede apreciar en el siguiente diagrama:

Obviamente, tal cosa no ocurre, lo que corrobora la inexactitud de las afirmaciones hechas por Rowbotham. Sobre la imagen siguiente podemos apreciar lo antedicho en conjunto:

Basándose en el diámetro de la Tierra calculado por Eratóstenes, Hiparco de Nicea, aproximadamente 150 años a. de J.C., calculó la distancia Tierra-Luna. Utilizó un método sugerido un siglo antes por Aristarco de Samos, el más osado de los astrónomos griegos, los cuales habían supuesto ya que los eclipses lunares eran debidos a que la Tierra se interponía entre el Sol y la Luna. Aristarco descubrió que la curva de la sombra de la Tierra al cruzar por delante de la Luna indicaba los tamaños relativos de la Tierra y la Luna. A partir de esto, los métodos geométricos ofrecían una forma para calcular la distancia a que se hallaba la Luna, en función del diámetro de la Tierra. Hiparco, repitiendo este trabajo, calculó que la distancia de la Luna a la Tierra era 30 veces el diámetro de ésta. Tomando la cifra de Eratóstenes, o sea, 12.000 km, para el diámetro de la Tierra, esto significa que la Luna debía de hallarse a unos 384.000 km de la Tierra. Este cálculo resultó ser bastante correcto

Aristarco realizó también un heroico intento por determinar la distancia Tierra-Sol. El método geométrico que usó era absolutamente correcto en teoría, pero implicaba la medida de diferencias tan pequeñas en los ángulos que, sin el uso de los instrumentos modernos, resultó ineficaz para proporcionar un valor aceptable. Según esta medición, el Sol se hallaba unas 20 veces más alejado de nosotros que la Luna (cuando, en realidad, lo está unas 400 veces más). En lo tocante al tamaño del Sol, Aristarco dedujo, aunque sus cifras fueron también erróneas- que dicho tamaño debía de ser, por lo menos, unas 7 veces mayor que el de la Tierra, señalando a continuación que era ilógico suponer que el Sol, de tan grandes dimensiones, girase en tomo a nuestra pequeña Tierra, por lo cual decidió, al fin, que nuestro planeta giraba en tomo al Sol.

En 1650 (mucho antes de que existiera la NASA), el astrónomo belga Godefroy Wendelin, repitiendo las observaciones de Aristarco con instrumentos más exactos, llegó a la conclusión que el Sol no se encontraba a una distancia 20 veces superior a la de la Luna (lo cual equivaldría a unos 8 millones de kilómetros), sino 240 veces más alejado (esto es, unos 97 millones de kilómetros). Este valor era aún demasiado pequeño, aunque a fin de cuentas, se aproximaba más al correcto que el anterior.

Kepler

Por otra parte, en el año 1609, el astrónomo alemán Johannes Kepler abría el camino hacia las determinaciones exactas de las distancias con su descubrimiento que las órbitas de los planetas eran elípticas, no circulares. Por vez primera era posible calcular con precisión órbitas planetarias y, además, trazar un mapa, a escala, del Sistema Solar. Es decir, podían representarse las distancias relativas y las formas de las órbitas de todos los cuerpos conocidos en el Sistema. Esto significaba que si podía determinarse la distancia, en kilómetros, entre dos cuerpos cualesquiera del  Sistema, también podrían serlo las otras distancias. Por tanto, la distancia al Sol no precisaba ser calculada de forma directa, como habían intentado hacerlo Aristarco y Wendelin. Se podía conseguir mediante la determinación de la distancia de un  cuerpo más próximo, como Marte o Venus, fuera del sistema Tierra-Luna.

En 1673, el método del paralaje dejó de aplicarse exclusivamente a la Luna, cuando el astrónomo francés, de origen italiano, Jean-Dominique Cassini, obtuvo el paralaje de Marte. En el mismo momento en que determinaba la posición de este planeta respecto a las estrellas, el astrónomo francés Jean Richer, en la Guinea francesa, hacía idéntica observación. Combinando ambas informaciones, Cassini determinó el paralaje y calculó la escala del Sistema Solar. Así obtuvo un valor de 136 millones de kilómetros para la distancia del Sol a la Tierra, valor que, como vemos, era, en números redondos, un 7 % menor que el actualmente admitido. Desde entonces se han medido, con creciente exactitud, diversos paralajes en el Sistema Solar. En 1931 se elaboró un vasto proyecto internacional cuyo objeto era el de obtener el paralaje de un pequeño planetoide llamado Eros, que en aquel tiempo estaba más próximo a la Tierra que cualquier otro cuerpo celeste, salvo la Luna. En aquella ocasión, Eros mostraba un gran paralaje, que pudo ser medido con notable precisión, y, con ello, la escala del Sistema Solar se determinó con mayor exactitud de lo que lo había sido hasta entonces. Gracias a estos cálculos, y con ayuda de métodos más exactos aún que los del paralaje, hoy sabemos la distancia que hay del Sol a la Tierra, la cual es de 150.000.000 de kilómetros, distancia que varía más o menos, teniendo en cuenta que la órbita de la Tierra es elíptica, al igual que la del resto de órbitas de todos los planetas de nuestro Sistema Solar

Anterior: Capítulo IV: La verdadera forma y magnitud de la Tierra
Siguiente: Capítulo VI: El movimiento del sol, concéntrico con el centro polar