A qué altura está el sol sobre la Tierra Plana?

Por John Phillips "El Inmortal",
"Paco" López 
y Sergio Chifflet

Por nuestro grupo, se viene discutiendo como se sacan los cálculos al sol, en una de esas, resurge el tema sobre aquel asunto de Eratostenes. ¿Qué realmente medía, la circunferencia de una tierra esférica, o la distancia al sol de una tierra plana?

Primera Parte: [Por John Phillips]

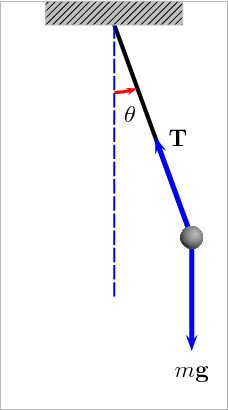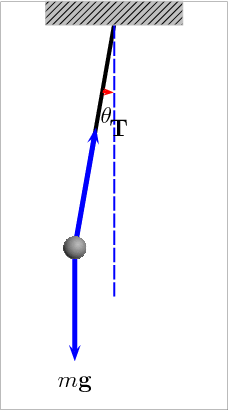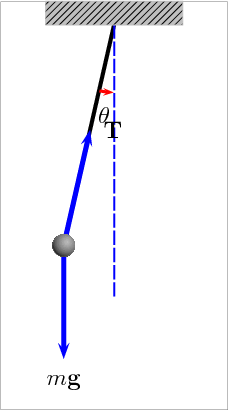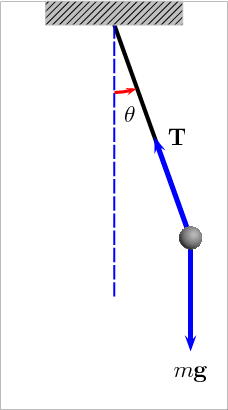
'Las sombras de Eratostenes', como le suelo llamar, nos pueden decir que realmente calculaba este señor, durante aquel solsticio de verano. (click sobre las imágenes para ampliarlas. Las imágenes NO están a escala)

Considerando la Tierra como una esfera (de hecho, no es una esfera totalmente perfecta), sin importar la medida de la vara, el vértice superior de la sombra en Alejandría, SIEMPRE hubiese tenido los 7.2° que se observaron. Incluso, al poner un edificio al lado, lo que cambia es el tamaño de la sombra, pero como se dijo, no el angulo del vértice superior, ya que los rayos del sol inciden de forma paralela. Pues es claro que se trataba con la curvatura terrestre.

Si la tierra es plana, el ángulo que observó Eratostenes en la sombra de la vara, en definitiva, tenía que estar relacionado con una altura de un sol cercano. Pero hay un grandísimo detalle aquí; ¿Cuanto medía la vara que utilizó Eratóstenes? ¿Y si pusiéramos un edificio al lado? Pues inevitablemente, el ángulo del vértice superior SIEMPRE va a cambiar según la medida de lo que ocasiona la sombra. Según el dato, el sol estaría poco más de 6000 km de altitud.

Así que; ¿Que nos dicen las sombras de dos objetos juntos, pero de muchísima diferencia en su tamaño? ¿Cambia el ángulo del vértice superior o siempre permanece igual aunque cambie el tamaño de la sombra?

Bueno, nosotros sabemos la respuesta, pero dejemos a los tierraplanistas que la descubran por ellos mismos.

Segunda Parte [Por Paco López]

Vaya! parece que en la planicie el experimento de Eratóstenes para hallar la altura del sol falla más que una escopeta de feria.

Para verlo, he replicado el experimento en tres ciudades distintas: Alejandría, Zaragoza y Londres. La primera porque es el lugar del experimento original del palito del griego y las otras dos, porque son ciudades que conozco y sé a la altura a la que se encuentra el sol durante el solsticio de verano

El resultado es sorprendente y es que resulta que en la planicie en la que vivimos, el sol puede estar a la vez y por lo menos... ¡A tres alturas completamente distintas!

No sé si nuestros amigos terraplanos tienen alguna explicación trascendental-metafísica-espiritual sobre esta pequeña incertidumbre, que parece ser que la ciencia ha sido incapaz de observar hasta la fecha, sin duda debido a los complejos cálculos utilizados y la precisión de los instrumentos de medida. A saber:

• Razones trigonométricas básicas
• A ojímetro, conociendo la latitud de las tres ciudades y Aswan.

Pues eso, chavales...que vivimos en un plano y el sol puede estar en tres sitios al mismo tiempo. ¿Cómo os quedáis?

Tercera Parte [Por Sergio Chifflet]
Todos sabemos, porque hemos ido a la escuela o porque lo hemos leído en la Demostración XII de la Tierra Esférica, que, durante los equinoccios (esto es el 21 de marzo y el 21 de septiembre) el sol cae justo sobre el ecuador y no provoca sombra alguna en el mediodía astronómico, mientras que en otras latitudes, la sombra proyectada se corresponde exactamente con la latitud del lugar

Muchos tierraplanistas de habla hispana provienen de estos lugares que he seleccionado, a los que además he agregado Ushuaia (aunque creo que no hay ningún creyente en la Tierra Plana por allá) por ser interesante su ubicación geográfica. En el mapa podemos ver la latitud correspondiente a cada lugar (o, lo que es lo mismo, el ángulo con el que llegan los rayos solares a cada sitio en los equinoccios) y su distancia al ecuador

Con estos datos intentaremos averiguar a qué altura se encuentra el sol sobre la Tierra Plana.

• San Francisco: 5414.6 km
• México DF: 6119.4 km
• Caracas: 6296.6 kim
• Santiago: 5623.3 km
• Ushuaia: 4295.3 km

Ahora, con estos valores haremos un gráfico sencillo, del que a simple vista podemos sacar la conclusión de que el sol aumenta su altura en las cercanías del ecuador, mientras que está más cerca de la superficie cuanto más nos alejemos sin importar que se trate del hemisferio norte o el sur, y por supuesto, como ya se ha dicho más arriba, el sol no puede tener varias alturas AL MISMO TIEMPO. Eso es sencillamente absurdo.

Entonces... ¿A qué altura está el sol sobre la Tierra Plana?

Consideraciones finales: [Por John Phillips]

Cómo las excusas nunca faltarán por parte de los defensores del Tierraplanismo, nos adelantamos al clásico 'argumento': 

"La diferencia no es por geometría porque la tierra no sea plana, es que 'la refracción atmosférica' cambia la posición del astro y hace que la sombra vaya de acuerdo a la latitud del observador."

Ese es otro de los tantos arriesgados comentarios (para ellos) que nos dejan, pues usemos un simple cálculo empírico para ver cómo quedaría el ángulo de elevación del sol, siguiendo el 'argumento' tierraplano. Así que personas NO simpatizantes a la tierraplana, ya tienen claro que este cálculo se hará en base a lo que ellos exponen y siguiéndoles el juego, por lo que usaremos algo simple y no entraremos en complicaciones ya que para los propósitos no vale la pena.

Esta es la ecuación básica de Bennet, en donde  es el ángulo de elevación, el resultado será en arco-segundos:

Para los siguientes ciudades que ya se mencionaron, la diferencia del ángulo será la siguiente:

• San Francisco: 46,32 arcsec
• México DF: 21,13 arcsec
• Caracas: 11,02 arcsec
• Santiago: 39,53 arcsec
• Ushuaia: 1,41 arcmin

Y seguimos igual, con grandísimas diferencias en las altitudes de un 'sol local' para una 'tierra plana', según cambiamos de latitud respecto con el ecuador. Si usted, terraplano que lee, dice que esto no es así, esperamos gustosamente sus papeles con los cálculos sobre refracción atmosférica, si va a decir que es 'imposible' hacer tal cosa, ni se moleste en contestar.

Otro comentario que ha surgido, es que el sol terraplanero, sube y baja, esto principalmente lo han sacado de los vídeos del sol de medianoche en regiones polares y según sea el caso, en donde el sol "sube" y "baja" a lo largo del día pero sin ocultarse.

Curiosamente, para quienes no estamos en esas regiones, no vemos tal cosa, y aplicándolo al caso que se viene considerando, en cualquiera de los equinoccios, no sucede así en nuestras regiones. Les pedimos a los Tierraplanistas, mejores argumentos que lo antes mencionado.

Astronomía Zetética (S. Rowbotham) Capítulo XIV - Variabilidad de las oscilaciones del péndulo

Por: John Phillips "El Inmortal"

Capítulo XIV: Examen de las llamadas "pruebas" de la esfericidad terrestre Variabilidad de las oscilaciones del péndulo Muchos sostienen que debido a que un péndulo oscila más rápidamente en la región norteña que en el ecuador, la Tierra está probada no solo como un globo, sino como que tiene un movimiento axial, y que la variación en la oscilación, es por el aumento gradual al acercarse al polo norte, se concluye que la verdadera forma de la Tierra es la de un esferoide oblato, el diámetro a través de los polos es menor que el del ecuador. Newton calculó la diferencia como la 235 parte del diámetro total, o que el polar era para el diámetro ecuatorial de 680 a 692. Huygens dio la proporción de 577 a 875, o una diferencia de alrededor de un tercio del diámetro total. Otros han dado proporciones todavía diferentes, pero recientemente la diferencia de opinión, cada uno el resultado del cálculo,se ha vuelto tan grande que muchos han llegado a la conclusión de que en lugar de achatada, la tierra realmente es un esferoide oblato. Se argumenta que a medida que la longitud de la oscilación de un péndulo de un segundo en el ecuador es de 39,027 pulgadas (‪99,1286‬ cm), y en el polo norte 39,197 pulgadas (‪99.56038‬ cm), que la Tierra, como una naranja, tiene una forma globular, pero algo aplanada en los "polos". Pero este supuesto argumento procede y depende de la suposición de que la Tierra es un globo que tiene un "centro de atracción de gravedad", hacia el cual todos los cuerpos gravitan o caen, y como un péndulo es esencialmente un cuerpo que cae bajo cierta restricción, el hecho de que cuando tiene la misma longitud oscila o cae más rápidamente en el norte que en el ecuador es una prueba de que la superficie norte está más cerca del "centro de atracción" o centro de la Tierra que la superficie ecuatorial: por supuesto, si está más cerca, el radio debe ser más corto, y por lo tanto la Tierra es "un esferoide achatado en los polos" Lo anterior es muy ingenioso y plausible, pero desafortunadamente por su carácter de argumento, la evidencia se brinda queriendo que la Tierra sea un globo; y hasta que se presente una prueba de convexidad, todas las preguntas en cuanto a que sean oblatas, oblongas o completamente esféricas, lógicamente están fuera de lugar. Es deber de aquellos que, desde el comportamiento de un péndulo en diferentes latitudes, afirman que la Tierra es esférica, para probar primero que ninguna otra causa podría operar además de una mayor proximidad a un centro de gravedad para producir las diferencias conocidas en sus oscilaciones. Esto no se hizo, ni se intentó, todo el asunto debe ser condenado como lógicamente insuficiente, irregular y sin valor para su propósito previsto. M.M. Picart y De la Hire, dos célebres savants franceses, así como muchos otros científicos, han atribuido las variaciones del péndulo a las diferencias de temperatura en diferentes latitudes. Es cierto que los cambios promedio de temperatura son más que suficientes para provocar las variaciones que se han observado. La siguiente cita mostrará los resultados prácticos de estos cambios: Todos los cuerpos sólidos con los que estamos rodeados están constantemente sometidos a cambios de volumen, correspondientes a las variaciones de temperatura ...La expansión y contracción de metales por calor y frío constituyen temas de atención seria y cuidadosa para los fabricantes de cronómetros, como se verá en las siguientes afirmaciones: - La longitud del péndulo que vibra en segundos, in vacuo , en la latitud de Londres (51° 31' 8" norte) a nivel del mar, y a la temperatura de 62° Fahrenheit , se ha comprobado con la mayor precisión que es 39.13929 pulgadas; ahora, como el metal del que está compuesto está constantemente sujeto a la variación de temperatura, no puede dejar de suceder que su longitud varía constantemente, y cuando se afirma además que si se "baja" el bob de 1 a 100 de pulgada, el reloj perderá diez segundos en veinticuatro horas; que la elongación de 1-1000 de pulgada hará que pierda un segundo por día; y que un cambio de temperatura igual a 30 ° Fahrenheit alterará su longitud de la 1-5000 parte, y ocasionará un error en la velocidad de avance de ocho segundos por día, parecerá evidente que se debe idear algún plan para obviar tan grave inconveniencia."  La temperatura media anual de toda la tierra a nivel del mar es de 50° Fahrenheit. Para diferentes latitudes es la siguiente:  De la tabla anterior se ve que la temperatura disminuye gradualmente desde el ecuador hacia el polo, lo que necesariamente contraería la sustancia del péndulo, o comenzando y haciendo que oscile más rápidamente. Además de la temperatura de una determinada latitud, se debe tener en cuenta la presión y la densidad del aire. En los números 294 y 480 de las "Transacciones Filosóficas", el Dr. Derham registra una serie de experimentos con péndulos al aire libre, y en el receptor de una bomba de aire, que resume de la siguiente manera: "Los arcos de vibración in vacuo eran más grandes que al aire libre, o en el receptor antes de que se agotara: la ampliación o disminución de los arcos de vibración eran constantemente proporcionales a la cantidad de aire , o rareza, o densidad de la misma, que quedaba en el receptor de la bomba de aire. Y como las vibraciones eran más largas o más cortas, el tiempo era en consecuencia: a saber, dos segundos en una hora cuando las vibraciones eran más largas, y cada vez menos cuando el aire era re -admitido, y las vibraciones acortadas ". Por lo tanto, es evidente que dos causas distintas y tangibles operan necesariamente para producir variabilidad en las oscilaciones de un péndulo en diferentes latitudes, sin tener que recurrir a un aplanamiento en los polos de un globo imaginario. En primer lugar, la disminución gradual de la temperatura a medida que el péndulo se transporta desde el ecuador a la región polar, tiende a acortar su longitud y, por lo tanto, a aumentar su número de oscilaciones por hora o por día; y segundo, cuando se acerca el centro polar, el aire es más frío, por lo tanto más denso, y por lo tanto los "arcos de oscilación" más cortos, y los tiempos de oscilación menores, o en otras palabras, el número de oscilaciones mayor en un período dado. También se ha determinado que el péndulo está influenciado por otras condiciones, por estados eléctricos y magnéticos de la atmósfera. Cuando existen condiciones eléctricas intensas, los arcos y los tiempos de oscilación son menores que durante la existencia de condiciones opuestas. Por lo tanto, si en diferentes latitudes se realizan experimentos de péndulo al vacío, a la misma temperatura y siempre a nivel del mar, las diferentes condiciones eléctricas y magnéticas prevalecientes inducirán resultados variables. La atención de algunos de los observadores más precisos y pacientes se ha dirigido a este modo de probar la forma oblata esferoidal de la tierra, pero los resultados nunca han sido satisfactorios, ni como se esperaba, o que la teoría de la rotundidad debería producir. Las siguientes observaciones sobre este tema son interesantes: "Newton fue la primera persona que hizo un cálculo de la figura de la tierra sobre la teoría de la gravitación. Tomó la siguiente suposición como la única a la que podría aplicarse su teoría. Asumió que la tierra era fluida. materia que asumió que era igualmente densa en cada parte... Para probar su teoría, supuso que la tierra fluida era un esferoide. De esta manera, dedujo que la forma de la tierra sería un esferoide en el que la longitud del más corto es la longitud del diámetro más largo o ecuatorial, en la proporción de 229 a 230." "La siguiente tabla comprende los resultados de los experimentos de péndulo más confiables que se han realizado hasta ahora, y entre los que se encuentra la extensa serie de observaciones del general Sabine". (Aquí se dan detalles de sesenta y siete experimentos hechos en cada latitud al norte del ecuador, desde 0° 1' 49" norte a 79° 49' 58" norte, y de veintinueve experimentos en el sur desde la latitud 0° 1' 34' sur, al Cabo de Hornos, 55° 51' 20" sur, y Shetland del Sur. 62° 56' 11" sur.) Tenemos aquí ante nosotros los resultados de cincuenta y cinco observaciones del péndulo de segundos, y de 76 observaciones del péndulo invariable; en todos los 131 experimentos; cuyo número, sin embargo, incluye ocho de los primeros y quince de los últimos, que difieren notablemente, en comparación con los resultados generalmente de los valores calculados. El general Sabine observa estas discrepancias que "se deben en mayor grado a las peculiaridades locales que a lo que se puede llamar más estrictamente errores de observación". Y ya el Sr. Bailey (en Memoirs of the Royal Astronomical Society, volumen 7), había expresado la opinión de que las oscilaciones de un péndulo se ven afectadas poderosamente, en muchos lugares, por la atracción local del sustrato sobre el que se balancea. , o por alguna otra influencia directa actualmente desconocida para nosotros, y cuyo efecto supera con creces los errores de observación". El propio general Sabine relata: - 'El capitán Foster fue amueblado con dos péndulos invariables de exactamente la misma forma y construcción que los que habían sido empleados por el capitán Kayter y yo. Ambos péndulos se hicieron vibrar en todas las estaciones, pero por alguna causa, que el Sr. Bailey no pudo explicar, las observaciones con uno de ellos fueron tan discordantes en South Shetland como para requerir su rechazo ". De las observaciones y citas anteriores, es obvio que la suposición de Sir Isaac Newton de que la Tierra es un esferoide oblato no está confirmada por experimentos realizados con el péndulo.

Rowbotham intenta decir que como la temperatura es un factor que altera el periodo de un péndulo, ya que con el calor la mayoría de los sólidos se dilatan y en este caso se alargaría la longitud del péndulo, haciendo el periodo de oscilación más lento; o por el contrario, con el frío se contraen, reduciendo la longitud y haciendo el periodo más rápido.

Pues hay más factores que la temperatura en si, relacionada con la longitud, como por ejemplo:

• Aceleración gravitatoria
• Fricción Pivote
• Presión
• Densidad del aire
• Humedad

Cómo en este caso lo que se expone con el péndulo es que la gravedad, que afecta la masa del mismo, pues al tener un periodo más rápido en el polo norte que al ecuador, hay una mayor aceleración por gravedad, y que por tanto, la tierra no es una esfera perfecta, más bien, un esferoide oblato.

Animación de un péndulo que muestra las fuerzas que actúan sobre el pendiente: la tensión T en la varilla y la fuerza gravitacional mg

Ya que Rowbotham estaba 100% 'convencido' que esto era una falacia, podemos usar la observación empírica, experimentable y repetible, de cronometrar la caída libre de los objetos según nos alejamos del ecuador hacia los polos.

Está ampliamente demostrado, que toda masa independientemente su densidad, va a cronometrar lo mismo en su caída libre en un mismo lugar, (si la fricción del aire lo impide, hágase al vacío el experimento o utilice otro tipo de material)

La observación empírica demuestra que en el polo norte, la masa acelera en su caída libre a razón de aproximadamente 9.8322 metros por segundo al cuadrado (9.8322 m/s²) a nivel de mar.

La observación empírica demuestra que en el ecuador, la masa acelera en su caída libre a razón de aproximadamente 9.7803 metros por segundo al cuadrado (9.7803 m/s² ) a nivel de mar.

Están pasando dos cosas, una; ya se dijo en lo que erradamente crítica Rowbotham, a mayor altura, menor aceleración de la masa en su caída libre, como la tierra no se considera como una esfera perfecta, sino un esferoide oblato, pues al estar "más altos" o más alejados del centro al ecuador, la aceleración es levemente menor que en los polos, y como ya deben saber, un péndulo genera energía potencial y energía cinética entre oscilaciones, la masa del péndulo al alcanzar su estado de energía potencial, sufre luego una caída libre, y pues es muy evidente que a nivel de mar en los polos, la masa del péndulo se verá acelerando en su caída libre más rápido que en el ecuador.

La otra es que si la tierra gira, esa aceleración centrípeta que tenemos al ecuador es de unos 0,03 m/s², entendiéndose porque la tierra es "achatada" en los polos, y porque la aceleración gravitatoria es levemente menor al ecuador.

Empíricamente, queda demostrado con lo mencionado, que un péndulo tiene un periodo más rápido en los polos por una mayor aceleración de la masa en su caída libre que al ecuador, y que no solo es por el asunto del largo menor por contracción debido al frío.

Una ecuación simple para el periodo es:

Donde L es la longitud del péndulo y g es la aceleración de la gravedad local

Solo considerando la aceleración gravitatoria en este caso y omitiendo lo demás para propósitos de entender lo que se viene explicando, al polo norte el periodo para un péndulo con un largo de 28 centímetros sería aproximadamente de:

2π*sqrt(0,18/9,8322)  ~ 0.850141

Al ecuador, el periodo para un péndulo con un largo de 28 centímetros sería aproximadamente de:

2π*sqrt(0,18/9,7803) ~ 0.852393

 

El modelo de "péndulo de gravedad simple" asume que no hay fricción ni resistencia al aire.

Efecto Allais

El efecto Allais es una supuesta precesión anómala del plano de oscilación de un péndulo durante un eclipse solar. Este efecto es inexplicable para los modelos estándar de gravitación de Física, pero publicaciones recientes tienden más bien a las explicaciones convencionales, que explican estas observaciones.

El efecto se observó por primera vez en el año 1954. Maurice Allais, un erudito francés que ganó el Premio Nobel en Economía, también observó este efecto en 1959 durante otro eclipse solar.

Durante el eclipse solar del 26 de enero de 2009, se encontró una correlación entre el comportamiento anómalo de un péndulo y de una balanza de torsión, situados en dos puntos diferentes fuera de la zona de sombra.

Ocho gravímetros y dos péndulos fueron desplegados en seis lugares de contraste en China durante el eclipse solar del 22 de julio de 2009. Aunque uno de los científicos implicados declaró en una entrevista haber observado el efecto Allais, el resultado no ha sido publicado en ninguna revista científica de referencia.

H. R. Salva utilizó un péndulo de Foucault automatizado y no encontró ninguna evidencia de un cambio de precesión del plano de oscilación del péndulo (de 0,3 grados/hora según Allais) durante el eclipse solar del 11 de julio de 2010.

Anterior: Capítulo XIV - La declinación de la Estrella Polar /  El "compás de proporciones"
Siguiente: Capítulo XIV - Arcos del meridiano

"8 pulgadas"

por John Phillips

¿De dónde salen las 8 pulgadas por milla cuadrada que usó Samuel Rowbotham? Pues bien, es una aproximación, si usamos a Pitágoras, encontramos en la primera imagen los siguientes valores:

K= Distancia en millas
Re= Radio Medio en millas
C = "Caída por curvatura"

5280/1 = para obtener el resultado en pies como se muestra en la primera imagen:

63360/1 = para obtener el resultado en pulgadas como se muestra en la siguiente imagen.

Una ecuación más aproximada tendría que ser 8,002021 pulgadas multiplicado por millas al cuadrado, pero el problema, es que esto es una operación incompleta, solo es el desnivel pasado el horizonte, y el valor cambiará según la elevación del observador. Por tal motivo, no puede haber una tabla fija con desniveles, a menos que se haga una por cada metro de elevación del observador.

Una buena aproximación para el caso de los kilómetros, es multiplicar 0,0785 metros por kilómetros al cuadrado.

Simplifiquemos ... Mil metros caben en un kilómetro, así que los dividimos entre el diámetro medio terrestre y nos sale ese valor constante de 0,0785 metros redondeados.

Una buena aproximación para hallar la distancia al horizonte es multiplicar 3,57 por la raíz cuadrada de la altitud del observador en unidades de metros. Por ejemplo, para un observador con una elevación de ojo a 1,80 metros sobre el nivel del mar, el horizonte le quedará aproximadamente a 4.8 kilómetros.

 

Usemos un ejemplo, los tierraplanistas tienen una tabla donde aseguran las "caídas por curvatura", por ejemplo, el caso para 5 km de distancia "tendría una caída" de:

0,0785*(5)^2 ~ 1,96 metros

(click en la imagen para ampliar)

Pero es un procedimiento incompleto si tienes a un observador elevado, la operación completa sería así de tener por ejemplo, una elevación (sobre el nivel del mar) de 1,8 metros:

0,0785*(5 - 3.57*sqrt(1,8))^2 ~ 0,35 centímetros de "caída" a 5 km de distancia.


Por supuesto, solo hablamos del cálculo geométrico sin contar con la refracción atmosférica. Para ello, usamos un coeficiente estándar de unos 0,16 (El coeficiente varía según el gradiente térmico vertical, la presión según la altura y la temperatura local, pero se usa el estándar para una referencia rápida.). Si la visión de nuestro observador está a 2 metros sobre el nivel del mar, entonces su horizonte está a 5 km aproximadamente.

Usando el coeficiente de refracción de la siguiente forma, nos dará el resultado de hasta dónde se extiende el horizonte, que ahora son unos: 5,5 km aproximadamente.

Luego, la zona oculta geométrica pasado el horizonte para ese observador, teniendo un objetivo alejado a 20 km será de:  17,5 metros aproximadamente.

De esta manera es que se aplica el coeficiente de refracción al valor constante, y ya nos sale el resultado incluyendo la refracción atmosférica, que un objetivo estará oculto por debajo de los 13,85 metros redondeado.

Se que esta parte se ve como complicada, pero esto lo dejará más claro, si usas el valor constante de 8 pulgadas, al incluir el coeficiente de refracción de 0,16 el valor constante cambia de 8 pulgadas a 6,72 pulgadas, que multiplicaras por millas al cuadrado. ¿Lo sabían terraplanistas?

Incluso, hacer ese procedimiento de multiplicar por distancia al cuadrado, solo sirve en cortas distancias, puesto que  eventualmente, el recorrido constante forma una parábola, no un círculo, para que lo entiendan mejor, pueden ir a esta applet que hice en Geogebra.

Ir a Geogebra