Astronomía Zetética (S. Rowbotham) Capítulo XIV: Línea tangencial del horizonte

por John Phillips

Capítulo XIV:  Línea tangencial del horizonte Si se coloca un teodolito "nivelado" en la orilla del mar, y se dirige hacia el mar, la línea del horizonte tendrá una cantidad por debajo de la cruz [hilos de la mira del teodolito], y una cierta "inclinación", o debería hacerse una inclinación [al teodolito] desde la posición del nivel para unir la cruz y el horizonte marino. Si el teodolito está fijado de manera similar, pero a una mayor altitud, el espacio entre la cruz, el horizonte marino, y la inclinación del instrumento para unirlos, también es mayor. De lo anterior mencionado, que es perfectamente cierto, se ha concluido que la superficie de la tierra es convexa, y que la línea de visión sobre el mar [Rowbotham escribió, ¨nivelada¨, entre comillas, como quien dice], sea tangencial. Como prueba de que no es el caso, se puede intentar el siguiente experimento:  fig.92 Coloca un teodolito en un punto elevado cerca del mar, "nivélalo", y dirígelo sobre el agua. Cuando el horizonte se vea un poco debajo de la cruz o el centro del telescopio, como se muestra en el diagrama, fig. 30, elija si la causa puede ser a saber, colimación o refracción.  Fig. 30                                                 Fig. 31 Ahora deje que el instrumento se incline hacia abajo hasta que la cruz toque el horizonte, como se muestra en la fig.31 , y en el siguiente diagrama, fig. 92. Si el teodolito tuviera un tubo simple sin lentes, en lugar de un telescopio, que es lo que causa la apariencia que se muestra [en la fig.30], el horizonte se vería alineado con la cruz o el eje del ojo, como en A, fig. 92, y la cantidad de "inmersión" requerida para poner la cruz y el horizonte en contacto entre sí, estará representada por el ángulo A, T, S, al que debe agregarse la colimación. En cada instancia donde el experimento ha sido especialmente probado, la caída, sin la colimación solo ascendió al ángulo A, T, S; probando así que la 'superficie del mar, S, B, es horizontal, porque es paralela a la línea A, T. Si el agua es convexa, la línea de visión, A, T, sería una tangente, y la inclinación a el horizonte sería T, H, representado por el ángulo A, T, H. Este ángulo, A, T, H, nunca se observa, pero siempre A, T, S, más la colimación o divergencia producida por las lentes en el telescopio del teodolito. Por lo tanto, la superficie de las aguas está de forma horizontal en todas partes. Las palabras "colimación", "divergencia", "refracción", etc, se han usado muchas veces en relación con esta parte del tema, y el siguiente simple experimento mostrará tanto lo que se quiere decir, como su influencia en la práctica. Tome una "lupa" o una lente convexa, y sosténgala sobre una línea recta dibujada sobre una hoja de papel. Si la línea se dibuja más larga que el diámetro de la lente, esa parte de ella que está fuera de la lente tendrá una posición diferente a la que se ve a través de ella, como se muestra en el siguiente diagrama fig. 93 fig.93 En lugar de que la línea vaya ininterrumpidamente a través de la lente en la dirección A, B, divergerá y aparecerá en 1, 2; o aparecerá por encima de la línea A, B, como en 3, 4, si la lente se mantiene a la mínima cantidad por encima o por debajo del centro real. Una lente es una lupa porque los objetos que se ven a través de ella, se dilatan o se extienden desde su centro. El punto infinitesimal o matemático que está en el centro, por supuesto, no está visiblemente influenciado, en el centro mismo está el verdadero eje del ojo, pero cualquier parte en el más mínimo grado de ese centro abstracto, está dilatado, o divergente, o arrojado más lejos de lo que sería a simple vista; de ahí su aparente ampliación o expansión, o lo que sea, por lo tanto, se magnifica. Realmente es así porque se arroja más o menos fuera del centro, y el poder de aumento o de disminución de la lente es realmente la más o menos divergencia de los rayos de luz al pasar a través de la sustancia de la que esta compuesto. En el telescopio de un teodolito, la cuadricula circular de la que está hecha la cruz se coloca en el centro real; por lo tanto, en una observación, no se ve el punto absolutamente opuesto a él, sino solamente otro punto minúsculo distante de él, cuya distancia se ve incrementada por la divergencia causada por las lentes; y esta divergencia es lo que se llama el "poder de aumento". Esta es la fuente de esas peculiaridades que se han considerado tan ilógicamente como pruebas de la rotundidad de la tierra. Es por esta peculiaridad que varios caballeros concluyeron prematuramente que el agua en el Canal de Bedford era convexa. El 5 de marzo de 1870, un grupo compuesto por los Sres. John Hampden, de Swindon, Wilts; Alfred Wallace, de Londres, William Carpenter, de Lewisham, MWB Coulcher, de Downham Market, y JH Walsh, editor del periódico "The Field", se reunieron en la orilla norte del "Old Bedford Canal" para repetir experimentos similares a los descrito en las figs. 2, 3, 4 y 5, en las páginas 11 a 14 de este trabajo. Pero, por causas que no necesitan ser mencionadas aquí, abandonaron sus intenciones originales y sustituyeron lo siguiente. En la cara oeste del Puente Old Bedford, en Salter's Lode, se colocó una señal a una altura de 13 pies y 4 pulgadas sobre el nivel del agua en el canal; a una distancia de tres millas, un poste de señal, con un disco de 12 pulgadas de diámetro en la parte superior, estaba tan fijo que "el centro del disco estaba a 13 pies y 4 pulgadas sobre la línea de flotación"; y a la distancia de otras tres millas (o seis millas en total), en el lado este del Puente Welney, se colocó otra señal, "3 pulgadas arriba del riel superior del puente, y 13 pies 4 pulgadas sobre el nivel del agua" Esta disposición se representa en el siguiente diagrama. fig 94. fig.94 A, la señal en el Old Bedford Bridge; B, el telescopio en Welney Bridge; y C, el poste de señal central, a tres millas de cada extremo. El cristal objetivo del telescopio tenía un diámetro de 4½ pulgadas; por lo tanto, el centro, o la línea del ojo verdadera, era 2¼ pulgadas más alta que la parte superior de la señal B, y 3¾ pulgadas debajo de la parte superior del disco de señal en C. Al dirigir el telescopio, "con una potencia de 50" hacia la señal A, cuyo centro estaba a 2¼ pulgadas debajo del centro del telescopio, se veía debajo; pero el disco en el polo central, cuya parte superior estaba, desde el principio, a 3¾ pulgadas por encima del centro, o la línea de visión, desde el telescopio, se veía considerablemente más alta que la señal A. De la cual, tres de las caballeros de inmediato, pero más inviables, llegó a la conclusión de que la elevación del disco en el campo de visión del telescopio se debió a un aumento en el agua del canal, mostrando la convexidad! mientras que no era nada más que simplemente la divergencia hacia arriba (de lo que ya estaba 3 pulgadas por encima de la línea de visión) producida por la potencia de aumento del telescopio, como se muestra en el experimento con la lente, en la fig 92. ¿Por qué omitieron considerar el hecho de que 3¾ pulgadas de exceso de altitud se realizarían con una potencia de aumento de 50, para parecer estar considerablemente por encima de la línea del ojo, y que una mera extensión de cabello, una cantidad que podría no ser detectado - hacia la señal distante, al aumentar, divergir o dilatarse por encima de ella, ¿parecería que se levantó por varios pies? ¿Por qué no se cuidaron de que la parte superior del disco central estuviera en línea con el telescopio y la señal distante, A? ¿Por qué, también,el centro del objeto de vidrio fue fijado 2¼ pulgadas más alto que el centro del objeto de observación en el otro extremo? No hubo dificultad para colocar el centro del telescopio, la parte superior del disco central y el centro de la marca de señal más alejada, a la misma altitud y, por lo tanto, en línea recta. Por su propio bien como caballeros, así como por el bien de la causa que se habían comprometido a defender, es lamentable que actuaran tan imprudentemente; que tan estúpidamente se pusieron a prueba de acusaciones de injusticia al arreglar las señales. ¿Ya habían visto lo suficiente como para demostrar que la superficie del agua era horizontal y, por lo tanto, sintieron instintivamente el deseo de hacer lo posible por retrasar el día de la denuncia general de su preciada doctrina de la rotundidad de la tierra? Tales preguntas son perfectamente justas en relación con una conducta tan injusta y unilateral. Es evidente que su ansiedad por defender una doctrina desafiada por otros venció su deseo de "verdad sin temor a las consecuencias"; y ansiosamente se apoderaron de la más veraz sombra de evidencia para sustentarse. En toda la historia de la invención, nunca se llegó a una conclusión más apresurada, mal concebida e ilógica; y es bueno para la civilización que tal procedimiento sea casi universalmente denunciado. Es apenas posible sacar una conclusión favorable en cuanto a sus motivos para apartarse de sus primeras intenciones. ¿Por qué no se limitaron a la repetición de los experimentos, un relato que yo había publicado anteriormente en el mundo, y para probar cuál fue la primera vez que se organizó la expedición? El de enviar un bote a una distancia de seis millas, y ver su progreso desde un punto fijo con un buen telescopio, los habría satisfecho por completo en cuanto a la verdadera forma de la superficie del agua; y como ninguna irregularidad en las altitudes de las señales, ni las peculiaridades de los instrumentos, pudieron haber influido en el resultado, todos los implicados deben haberse sometido inmediatamente a la verdad simple desarrollada por el experimento más simple posible. Que los hombres se aferren a la complicación, y lo prefieran a la simplicidad de acción, es difícil de entender, excepto por el principio, como se dijo en la antigüedad, "Algunos aman la oscuridad mejor que la luz". Es cierto que muchos están siempre dispuestos a luchar hasta la muerte por sus meras opiniones, que tienen poco o ningún respeto por la verdad real, por importantes que sean sus características o por su carácter sagrado. Estos mismos caballeros probaron otro experimento, del cual ellos, tan prematura e ilógicamente como antes, llegaron a la conclusión de que el agua era convexa y no horizontal. "Un nivel de Troughton de 16 pulgadas, ajustado con precisión, se colocó en la misma posición y sobre la misma altura del agua que el telescopio acromático grande empleado en el último experimento", cuando el poste de señal, a tres millas, y la bandera de señal en el el puente, a seis millas, se veía como se muestra en el siguiente diagrama, fig. 95. A es la cruz, B el señal-disco, y C la bandera de señal en el Old Bedford Bridge. El telescopio, D, D, D, que lleva la cruz A, está en el puente de Welney, a tres millas del anverso de B y seis de C. Fig. 95 De las observaciones anteriores, dos de los experimentadores llegaron a la conclusión de que la línea cruzada en la línea de visión era una tangente, y el agua convexa, la aparición de B y C, como resultado de la declinación de la superficie del canal . Ya se ha demostrado que los instrumentos de nivelación mejor construidos producen necesariamente, a partir de la naturaleza y disposición de las lentes, una refracción o divergencia de 1-1000 de un pie en una distancia de 10 cadenas o 660 pies, de modo que el bien conocido y la refracción admitida, inseparable de los instrumentos empleados, es completamente suficiente para explicar la posición del disco en B, y la bandera en C, sin exigir que la teoría de la rotundidad de la tierra sea corroborada. Es deber de los encuestadores, y todos los que tienen interés en este tema, estudiar cuidadosamente estas peculiaridades de los instrumentos de nivelación, y no solo para familiarizarse con ellos, sino para reconocer su influencia en cada una de sus operaciones. Si alguien tiene la más mínima duda del efecto de las lentes en la causa de la divergencia de la línea de visión, permita que simplemente proporcione dos instrumentos exactamente de la misma construcción, excepto que se le quitarán las lentes. Entonces se verá que el instrumento con lentes no leerá, sobre un bastón graduado, el mismo punto que sin ellos. Este último dará la lectura verdadera; y la diferencia entre esto y la lectura del instrumento con lentes, es la cantidad por la cual debe hacerse la concesión; de lo contrario, los resultados, aunque sean extensos e importantes, deben ser falaces. En relación con esta parte del tema, será útil explicar cuál es la causa del aumento aparente de un plano o superficie horizontal hacia el eje del ojo. En el siguiente diagrama, Fig. 96 A, B, representa una superficie plana, digamos varias millas sobre el mar, desde la orilla, y E, sea el ojo de un observador. Es evidente que mirando directamente hacia abajo, desde E hasta A, la posición real y aparente de la superficie del agua será la misma. Pero si se levanta una pantalla transparente o un pedazo de vidrio a cierta distancia del ojo, como en C, D, y la vista se dirige sobre el agua a la distancia W, la línea de visión cortará la pantalla C, D, en el punto 1, y la superficie del agua aparecerá en 3, igual a la altitud de 1. Si la vista se dirige ahora al punto X, la línea de visión, E, X, cortará la pantalla C, D , en el punto 2, y la superficie del agua aparecerá elevada al punto 4. Es evidente, entonces, que la línea de visión puede dirigirse más y más sobre el agua más allá de X, y cada línea adicional de la vista cortaría la pantalla más cerca de la línea E, C, H, pero nunca podría ser perfectamente paralela a ella. De la misma manera, la superficie del agua aparecería más y más cerca de la línea E, H, en H, pero nunca podría entrar en contacto real con ella: el ángulo H, E, X, se vuelve más y más agudo a medida que la distancia aumenta; pero, matemáticamente, las líneas E, X, E, H, podrían prolongarse ad infinitum, el ángulo C, E, 2, infinitamente agudo, y el espacio H, 4, entre la superficie de la oblea y la línea E, H , inconmensurablemente pequeño, pero el contacto real es matemáticamente imposible. Aunque siempre hay, a grandes distancias, un espacio de un minuto entre la línea de visión y la superficie del agua en el horizonte, aún así, para todos los propósitos prácticos, y a simple vista, no se requiere inmersión. Las observaciones anteriores se hacen considerando que el agua está quieta, como si estuviera congelada; pero como el agua del mar siempre está en un estado de ondulación, es evidente que una línea de visión que pasa sobre un horizonte marino no puede continuar matemáticamente paralela al plano del agua, sino que debe tener una inclinación diminuta hacia arriba en la dirección del cenit Por lo tanto, es frecuente que, cuando el sol se está ocultando sobre un mar tormentoso o muy crecido, el fenómeno de la puesta del sol comience en un punto del horizonte sensiblemente inferior a 90 ° desde el cenit. El mismo fenómeno se puede observar al amanecer, desde cualquier eminencia sobre el mar en dirección este, desde la cima de la colina de Howth, y la roca llamada "Ojo de Irlanda", cerca de Dublín, mirando hacia el este sobre la bahía de Liverpool, en la dirección de la costa de Lancashire. Esto se ilustra mediante un diagrama fig: 97 Fig. 97 A, D, B representa la superficie horizontal del mar, y D 1 y D 2, el ascenso óptico o aparente del agua hacia las líneas de los ojos O 1 y O 2; O, D, el observador; Z, el cenit; H, H, el horizonte; y S, S, el sol de la mañana y el de la tarde. Es obvio a partir de este diagrama que si el agua tuviera un carácter fijo, como cuando está congelado, el ángulo Z, O 1, o Z, O 2, sería uno de 90 °; pero a causa de las olas y rompientes en el horizonte H, H, montando la mitad de sus altitudes por encima de las líneas O 1 y O 2, la línea de visión se encuentra con el sol en S, que parece elevarse o asentarse en el horizonte elevado H, siendo el ángulo Z, O, S, inferior a 90 °. Esto es evidentemente la causa de la puesta del sol y el aumento en el mar, más tarde cuando el agua está en calma, y ​​antes cuando está muy perturbado, un hecho bien conocido por los viajeros que van al mar y los residentes en orillas orientales u occidentales. También es la causa de que el sol se levante más tarde y se coloque antes de lo que lo haría sobre un plano liso de la tierra, o sobre aguas absolutamente quietas, o de lo que debería hacer matemáticamente por su altitud conocida.

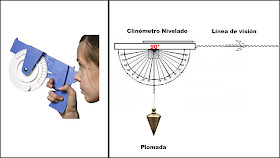
Este asunto es mas simple de lo que parece, vamos a resumirlo. Aquí Rowbotham vuelve con el fallido argumento de que el horizonte sube siempre al nivel de los ojos, tema que quedó muy aclarado en esta publicación, (Ir a la publicación). Para que se entienda el asunto de los teodolitos, decimos que cuando tenemos un angulo recto (90 grados) entre la linea de visión y lo que estemos usando, ese instrumento está a nivel. Por ejemplo, un clinómetro casero es un simple instrumento con un transportador, y un hilo con una plomada o un peso. Cuando tenemos un angulo recto (90 grados) entre la línea de visión y el hilo con la plomada, el clinómetro está nivelado.

Y podemos calcular cuantos grados verticales de desnivel tiene un objetivo que esté por arriba o por abajo de la línea de visión nivelada, como se muestra en esta otra imagen.

Un teodolito sigue el mismo principio, solo que la precisión de la medida del desnivel es por mucho mayor que en el caso de un clinómetro. Y por supuesto, también podemos considerar ángulos horizontales, no solo los verticales. Pero para el caso de la curvatura terrestre, y lo que Rowbotham dice, solo nos concentraremos en el desnivel y el angulo vertical.

Cuando tenemos nivelado un clinómetro o un teodolito, podemos usar la linea de visión como referencia para el desnivel, y el instrumento se convierte en un punto de tangencia como se ilustra a continuación.

¿Que nos puede mostrar un teodolito (nuestro punto de tangencia) completamente nivelado posicionado en la playa, y con vista al horizonte a través del agua? Nos puede mostrar que si la tierra es plana, a poca altura, el horizonte estará muy cerca del hilo axial del teodolito.

Sin embargo, si la Tierra es esférica, nuestro teodolito nivelado (punto de tangencia), mostrará el horizonte con un desnivel vertical, y aparecerá por debajo del hilo axial.

Otro detalle importante es que cuando tenemos un punto de tangencia como un teodolito, y consideramos esa linea de visión, jamás encontraremos el horizonte en la Tierra esférica, solo encontraremos el desnivel. Si queremos encontrar el horizonte, tendremos que bajar la mira de nuestro teodolito unos muy pocos grados hasta coincidir con el horizonte, pero el teodolito ya no estará nivelado, ni tendrá un ángulo recto, ahora el horizonte es el punto de tangencia, por eso el nombre del título de este capitulo.

Pues como se muestra en este video (Ir al video), son constantes las vistas del horizonte por debajo del hilo axial de un teodolito completamente nivelado, en la siguiente capturas del video, vemos que el angulo vertical (VA -Vertical Angle-) del teodolito al coincidir con el horizonte no son 90 grados, por lo que ni está nivelado, ni se le puede considerar como un punto de tangencia. Luego, cuando se nivela el teodolito (VA = 90 grados), entonces si es un punto de tangencia, y el horizonte aparece por debajo del hilo axial, cosa que solo puede ocurrir de la Tierra ser esférica.

Pues a eso hace referencia Rowbotham con esta ilustración.

Fig. 30                                                 Fig. 31

Ante la imponente e innegable evidencia de que la Tierra no es plana, este sujeto se las ingenió para ¨refutar¨ que eso sea alguna evidencia sustancial, y de paso criticar el excelente experimento realizado por Alfred Russel Wallace en el Old Bedford (Ir a la publicación). Pues bien, la excusa sigue así, Rowbotham indicó que como el uso de lentes convergentes, o convexos, cambiaban el tamaño de una línea, que necesariamente los teodolitos distorsionaban el horizonte (verticalmente) para que se viera por debajo del hilo axial, y eso nos hiciese pensar que se trataba de un desnivel.

Por ejemplo, el decía que al usar una lupa o un lente convexo, la linea original A,B de esta ilustración, se acortaba en 1,2 y en 3,4. Que son zonas adentro del lente y fuera del centro del lente.

Sin embargo a nuestro amigo Rowbotham se le escapa, que eso ocurre también si la linea cruza el centro del lente, ¿Porqué? Por que sin saberlo, Rowbotham estaba describiendo lo que hoy se conoce por FOV o (Field of View) de una lente. A mayor convexidad en el lente, mayor campo visual tendremos, pero también mayor distorsión, así que una linea mas larga que el diámetro de un lente convergente, puede (caber) en el campo del lente (FOV). Dicho por el mismo Rowbotham: ¨El horizonte siempre sube al nivel de los ojos¨.

Eso quiere decir que el teodolito al ser nivelado y ser un punto de tangencia, la linea del horizonte siempre debe coincidir con el hilo axial o la linea central del lente del teodolito. Y según las propias palabras de Rowbotham en este capitulo:

¨El punto infinitesimal o matemático que está en el centro, por supuesto, no está visiblemente influenciado, en el centro mismo está el verdadero eje del ojo, pero cualquier parte en el más mínimo grado de ese centro abstracto, está dilatado, o divergente, o arrojado más lejos de lo que sería a simple vista.¨

En otras palabras, como dijo alguna vez Iru Landucci: ¨Lo que está al centro (del lente) es lo que no tiene distorsión.¨ (Palabras de Landucci, haciendo referencia al caso de la distorsión de los lentes Fish Eye).

Pues me vuelvo a preguntar ... Si la linea del horizonte siempre coincide con nuestros ojos según Rowbotham, ¿como es que no coincide con el centro del lente del teodolito nivelado? Por que volviendo a repetir sus palabras, la distorsión del lente ocurre por arriba o por abajo del centro, y mientras mas se aleja del centro, mayor distorsión. Eso quiere decir que la linea del horizonte desde un comienzo, no coincide con el hilo axial o el centro del lente, donde no debería distorsionar. Otra grandísima incongruencia, es que su explicación da a entender de forma clara, que la distorsión solo ocurre para el caso del agua y del horizonte, ¿Porqué? Recordemos que esta es la vista que debemos tener en una tierra plana, en donde cerca de la superficie, el horizonte sube al nivel de los ojos, por tanto, coincide con el hilo axial o el centro del lente del teodolito.

Volvemos a repetir lo que dijo Rowbotham: ¨el centro por supuesto no está visiblemente influenciado, en el centro mismo está el verdadero eje del ojo¨ ¿Como es entonces que se distorsiona el horizonte verticalmente para que baje? Si para comenzar, el mismo debería estar al centro. ¿Y como es que solo baja el horizonte, porqué no suben los objetivos que aparecen por arriba del centro? ¿Se imaginan? Tendríamos lo mismo pero así:

Pero en fin, no vamos a hacer un drama por eso, vamos a tomarle la palabra momentáneamente a este señor, y dejemos el uso de lentes para evitar ser ¨engañados¨ por los mismos. Usemos otros métodos que no requieran lentes y solo el uso de nuestros ojos, solo que no vamos a estar cerca de la superficie, busquemos altura como en una montaña y hagamos lo que aparece en el experimento de la imagen.

Este es el video para los interesados:

El instrumento puede ser reemplazado por un clinómetro, o cualquier idea presentada en este hilo de Metabunk (Ir a Metabunk). Por supuesto, no estamos usando lentes, nuestro instrumento estará nivelado y será nuestro punto de tangencia, según Rowbotham, el horizonte va a subir al nivel o a la linea de vision del instrumento, pero en la realidad ... ¡Volvemos a ver el horizonte por debajo de nuestro punto de tangencia! Lo que daría por ver la cara de este señor de estar vivo, y las nuevas excusas que pondría ante tal evento, sabemos demasiado bien, lo ¨escapistas y trapecistas¨, que son estos personajes de la tierraplana, para escaparse de las evidencias. Pero bueno mis queridas y queridos lectores, buena salud para todos.