Estando en un tren se mueven con rapidez, arrojar un proyectil hacia delante, o en la dirección en la que el tren está en movimiento. Repetir luego, pero en la dirección opuesta; y se encontrará que la bala u otro proyectil siempre irá más lejos en el primer caso que en el segundo.
Si una persona salta hacia atrás desde un caballo en pleno galope, no puede saltar una distancia tan grande como la que conseguiría saltando hacia adelante. Saltando de un trineo en movimiento, hacia atrás o hacia adelante, se obtendrán los los mismos resultados.
Muchos otros casos prácticos podrían citarse para demostrar que cualquier cuerpo proyectado desde otro cuerpo en movimiento, no presenta el mismo comportamiento como lo hace cuando se proyecta a partir de un cuerpo en reposo. Tampoco son los resultados de la misma cuando se proyecta en la misma dirección que aquella en la que se mueve el cuerpo, como cuando se proyecta en la dirección opuesta; porque, en el primer caso, el cuerpo proyectado recibe su impulso de la fuerza de proyectil, además de que dada a él por el cuerpo en movimiento; y en el último caso, este impulso, menos la del cuerpo en movimiento. Por lo tanto, si la tierra fuera un globo, y se moviera rápidamente de oeste a este, un cañón disparado en una dirección este, debería enviar una bala a una distancia mayor de lo que resultaría disparando en dirección oeste. Pero los artilleros más experimentados -muchos de los cuales han tenido una gran práctica, tanto en el país como en el extranjero, en casi todas las latitudes- han declarado que ninguna diferencia es observable. Que apuntando con sus armas, no existe diferencia en el resultado en ningún punto de la brújula. Artilleros en los buques de guerra han notado una diferencia considerable en los resultados de sus disparos de armas de fuego en la proa, al navegar rápidamente hacia el blanco, y al disparar desde cañones colocados en la popa mientras navegan alejándose de éste, y en ambos casos los resultados son diferentes a los observados cuando se dispara desde un barco en perfecto descanso. Estos detalles de la experiencia práctica son totalmente incompatibles con la suposición de una tierra que gira. (...)
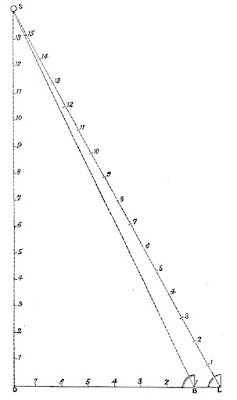
La respuesta dada por los defensores de la teoría del movimiento de la Tierra es la siguiente: Admitiendo que una bala despedida de la tierra en reposo alcanzaría, por ejemplo dos millas, la misma bala, disparada desde la tierra en movimiento, alcanzaría, tres millas; pero durante e tiempo que el proyectil está en el aire, la tierra habrá avanzado una milla en la misma dirección. Éste milla al ser deducida de las tres millas, que la pelota pasa realmente a través del aire, resulta en que prácticamente la distancia a la que se proyecta una bala es precisamente la misma en un tierra en movimiento o en una tierra en reposo. En el siguiente diagrama, Fig. 50, ilustrarán la trayectoria de una bola en las condiciones anteriormente descrito.
 |
| Fig. 50 |
La línea curva
A-B, representa la distancia que una bala volaría desde un cañón colocado en
A, sobre la tierra, en reposo.
A-C representa la distancia que la misma bala volaría como resultante de la acción conjunta del impulso en el cañón,
A, y la rotación de la tierra en la dirección
A-C. Durante el tiempo que la bala requeriría para atravesar la línea
A-C, el movimiento de la tierra llevaría al cañón hasta el punto
D; por lo tanto, la distancia
D-C, sería la misma que la distancia
A-B.
La explicación anterior es muy ingeniosa, y sería perfectamente satisfactoria si otras consideraciones no estuvieran involucradas en ella. Por ejemplo, la explicación anterior no prueba el movimiento de la Tierra -que simplemente supone que; pero como en todos los demás casos en que se describe el resultado de suponer, se crea un dilema. Exige que durante el tiempo que la bala está en el aire, el cañón está avanzando en la dirección del supuesto movimiento de la Tierra. Pero considerando las condiciones exigidas en los experimentos representados por las
figuras 47, 48 y 49, Si el cañón se dispara verticalmente, la bala caerá verticalmente, volviendo a la posición del cañón, por lo tanto, ese cañón no puede haber avanzado, por lo que la tierra no puede haberse movido.
Experimento 4.
(...) La superficie de la tierra es muy irregular en su contorno, con montañas que se elevan a varias millas sobre el mar, y que van a cientos de millas en todas las direcciones posibles; rocas, cabos, acantilados, gargantas, desfiladeros, cavernas, bosques inmensos, y toda otra forma de aspereza e irregularidad calculada para adherirse y arrastre a lo largo de cualquier medio puedan existir sobre ella: y si se trata de un globo girando sobre su eje, con la inmensa velocidad en el ecuador de más de mil millas por hora, es extremadamente difícil, si no imposible, concebir una tal masa en movimiento a una velocidad tal, y no teniendo la atmósfera junto con él. Cuando se considera, también, que el medio que se dice rodea la tierra y todos los cuerpos celestes, y llenando todos los grandes espacios entre ellos, es casi demasiado etéreo y sutil para ofrecer ninguna resistencia sensible, es todavía más difícil de entender cómo se puede la atmósfera que se traslade con la rapidez de la superficie giratoria de la tierra. Para estudiar los detalles de la neumática o hidráulica, no podemos sugerir un experimento que demuestre la posibilidad de tal cosa. Por lo tanto nos vemos obligados a concluir que si la tierra gira, la atmósfera gira también, y en la misma dirección. Si la atmósfera se precipita hacia adelante de oeste a este continuamente, estamos obligados de nuevo a la conclusión de que lo que flota o se suspende en ella, a cualquier altitud, lleva necesariamente un movimiento hacia el este. Un trozo de corcho, o cualquier otro cuerpo flotante en aguas tranquilas, serán inmóvil, pero dejar que el agua se pone en movimiento, en cualquier dirección que sea, y los cuerpos flotantes se moverán con él, en la misma dirección y con la misma velocidad. (...) Por tanto, si la atmósfera de la Tierra está en constante movimiento de oeste a este, todos los diferentes estratos que se sabe que existen en ella, y todos los diferentes tipos de nubes y vapores que flotan en ella deben moverse necesariamente rápidamente hacia el este. Pero, ¿cuál es el hecho? Si fijamos en cualquier estrella como un estándar o de referencia fuera de la atmósfera visible, es posible que a veces observar un estrato de nubes que viajan durante horas en una dirección lo opuesto a aquella en la que se supone que la tierra que se mueve.
 |
| Fig. 51 |
Ver la Fig. 51, que representa una sección de un globo, rodeado de una atmósfera, que se mueve a la velocidad de 1042 millas por hora en el ecuador, y en la dirección de las flechas
1,
2,
3, mientras que una corriente de nubes se están moviendo en la dirección opuesta, como se indica por las flechas,
4,
5,
6. No sólo se puede ver una capa de nubes que se mueven rápidamente de este a oeste, pero en el mismo momento otros estratos menudo puede ser visto en movimiento de norte a sur y de sur a norte. Es un hecho bien conocido por los aeronautas, que varios estratos de aire atmosférico a menudo se mueven en varias direcciones diferentes al mismo tiempo. Es el conocimiento de este hecho que lleva a un aeronauta experimentado, cuando se desea subir en el globo, y para ir en una dirección determinada, no considerar la forma en que el viento sopla sobre la superficie inmediata de la tierra, porque él sabe que a mayor altitud, puede estar pasando en ángulo recto, o incluso en contrario y de diversas maneras al mismo tiempo. (...)
En casi cualquier luz de la luna y de la noche nublada, puede verse no sólo que diferentes estratos se mueven en diferentes direcciones con diferentes velocidades; algunos flotando más allá de la cara de la luna rápida y uniformemente, y otros que pasan suavemente a lo largo, o a veces permaneciendo estacionarios. Algunos de los que han ascendido en globos para fines científicos han registrado que a medida que han pasado rápidamente a través de la atmósfera. Estos cambios se han observado tanto en ascenso y descenso, así como al ir por millas junto a la misma altitud. (..:)
Tal estado de la atmósfera sólo es compatible con el hecho de que otra evidencia ha demostrado, que la tierra está en reposo. (...)
A pesar de que la experiencia de toda práctica, y los experimentos todas especialmente instituidos están en contra de la posibilidad de un movimiento de tierra, y un movimiento independiente y la atmósfera que no se mueve, muchos matemáticos han tratado de "demostrar" que con respecto a esta tierra, tal era realmente el caso.
El argumento que participan en las observaciones precedentes contra la rotación de la Tierra a menudo se ha cumplido por la siguiente, a primera vista, la declaración plausible. Un barco con un número de pasajeros que van rápidamente en una dirección constante, al igual que la atmósfera de la tierra, sin embargo, podría tener sobre su cubierta de una serie de objetos que se mueven claramente y de diversas maneras, como las nubes en la atmósfera. Las nubes en la atmósfera se comparan con los pasajeros en la cubierta de un barco; hasta ahora los casos son suficientemente paralelo, pero los pasajeros son seres sensibles, que tiene dentro de sí mismos el poder de movimientos distintos e independientes: las nubes son el reverso; y aquí el paralelismo falla. Uno de los casos no es ilustrativo de la otra, y la suposición de rotación de la tierra permanece sin un solo hecho o argumento a su favor. Pájaros en el aire, o los peces y reptiles en el agua, habrían ofrecido un caso paralelo e ilustrativo, pero éstos, al igual que los pasajeros en la cubierta del barco, son seres sensibles e independientes; nubes y vapores son dependientes y no sensible, y deben por lo tanto de la necesidad moverse con, y en la dirección de, el medio en el que flotan.
Todo realidad observable en la naturaleza; todos los argumentos proporcionados por el experimento; cada proceso legítimo de razonamiento; y, al parecer, todo lo cual es posible que la mente humana prácticamente a concebir, se combinan en evidencia en contra de la doctrina del movimiento de la tierra sobre ejes.
Los experimentos anteriores y observaciones, lógicamente y matemáticamente suficientes como prueba contra el movimiento supuesto de la tierra en una órbita alrededor de la sol. Es difícil, si no imposible, para entender cómo el comportamiento de la pelota lanzada desde una pistola vertical debe ser otra en relación con el movimiento hacia adelante de la Tierra en el espacio, en lo que se refiere a su movimiento sobre los ejes. Además, es demostrable que no se mueve sobre ejes, y por lo tanto, la suposición de que se mueve en una órbita, es completamente inútil para los propósitos teóricos. La explicación de los fenómenos, para el que se enmarca la teoría del movimiento orbital y diurna, ya no es posible con un mundo globular corriendo a través del espacio en una vasta órbita elíptica, pero sin rotación diurna. De ahí que supone el movimiento orbital de la Tierra es lógicamente vacío, (...) pero ningún punto se puede tomar sin evidencia directa y práctica, vamos a ser juzgado el siguiente experimento.
Tomar dos tubos metálicos cuidadosamente alineados de no menos de seis pies de largo, y colocarlos en los lados opuestos de un marco de madera o un bloque sólido de madera o de piedra: Ajustarlos de tal manera que sus centros o ejes de visión deberán ser perfectamente paralelos entre sí. El siguiente diagrama muestra el arreglo.
 |
| Fig. 52 |
Ahora, dirigirlos al plano de alguna estrella fija notable, unos segundos antes de su hora del meridiano. Un observador se destacará en cada tubo, como en
A, B; y el momento en que la estrella aparece en el tubo
A-T, que se dé un fuerte golpe u otra señal, que se repiten por el observador en el tubo
B-T, cuando se ve por primera vez la misma estrella. Un período distinto de tiempo transcurrirá entre las señales dadas. Las señales se siguen unos a otros en una sucesión muy rápida, pero aún así, el tiempo entre que es suficiente para mostrar que la misma estrella,
S, no es visible en el mismo momento por dos líneas paralelas de vista
A-S, y
B-C. Una ligera inclinación del tubo,
B-C, hacia el primer tubo
A-S, se requeriría para la estrella,
S, para ser vistos a través de los dos tubos en el mismo instante. Deje que los tubos permanecen en su posición durante seis meses; al final de cuyo tiempo la misma observación o experimento producirán los mismos resultados la estrella,
S, serán visibles al mismo tiempo meridiano, sin la más mínima alteración que se requiera en la dirección de los tubos: de la que se concluye que si la tierra se hubiera movido, sería necesario ajustar la ligera inclinación del tubo,
B-C, que había requerido anteriormente. Pero como como tal ajuste no es necesario, la conclusión es inevitable, que en seis meses un meridiano dado sobre la superficie de la tierra no se mueve, y por lo tanto, que la tierra no tiene el menor grado de movimiento orbital.
Copérnico requiere, en su teoría de los movimientos terrestres, que la tierra se movió en una extensa trayectoria elíptica alrededor del sol, como se representa en el siguiente diagrama,
 |
| Fig. 53 |
donde
S es el sol,
A, la tierra en su lugar en junio, y
B, su posición en diciembre; cuando se desee ofrecer alguna prueba de este movimiento orbital sugirió que una estrella dada debe ser seleccionado para su observación en una fecha determinada; y en seis meses después, se debe hacer una segunda observación de la misma estrella. La primera observación
A-D, Fig. 53, se registró; y en la observación de nuevo al final de seis meses, cuando se suponía que la Tierra había pasado a
B, el otro lado de su órbita, ante el asombro de los astrónomos reunidos, se observó la estrella exactamente de la misma posición,
B-C, como lo había sido seis meses antes! Se esperaba que sería visto en la dirección
B-D y que esta diferencia en la dirección de observación demostraría movimiento de la Tierra de la
A a
B, y también proporcionar, con la distancia
A-S-B los elementos necesarios para el cálculo de la distancia real de la estrella
D.
El experimento anterior se ha intentado muchas veces, y siempre con el mismo resultado general. Ninguna diferencia lo que se ha observado en la dirección de las líneas de visión
A-D y
B-C, mientras que todos los principios conocidos de la óptica y la geometría requeriría, que si la tierra realmente se hubiera movido de
A a
B, la estrella fija
D, debe ser visto en la dirección
B-D. Los defensores de esta hipótesis de movimiento orbital, en lugar de ser satisfecho, de la falta de detectar una diferencia en el ángulo de observación, de que la tierra no podría haber cambiado su posición en el seis meses, fueron lo que independientemente de toda consistencia lógica, que en lugar de admitir y aceptar las consecuencias, ellos, o algunos de ellos, la mayoría indignamente declararon que no podían reproducir lo que dicta la teoría, a causa de su valor aparente para explicar ciertos fenómenos, afirmando que la distancia a la estrella
D, era tan inmensamente lejana, que, a pesar de que la tierra debe haberse movido de
A a
B, este gran cambio de posición no le daría una diferencia legible en el ángulo de observación en
B.
Desde la época de los experimentos anteriores, muchos han declarado que se ha detectado una cantidad muy pequeña de "paralaje anual". Sin embargo, la proporción dada por diferentes observadores ha sido tan diferentes, que nada definitivo y satisfactorio todavía pueden decidirse. Tycho Brahe, Kepler y otros, rechazaron la teoría de Copérnico, principalmente a causa del fracaso para detectar el desplazamiento o la paralaje de las estrellas fijas. (...)
La complicación, la incertidumbre y el estado insatisfactorio de la cuestión del paralaje anual, y por lo tanto del movimiento de la Tierra en una órbita alrededor del Sol, como lo indican los párrafos anteriores, son a la vez y para siempre aniquilado por el simple hecho, experimentalmente demostrable, que sobre una línea de base de una sola yarda, puede encontrarse un paralaje, tan cierta y tan grande, si no mayor, que la que los astrónomos pretenden encontrar con el diámetro de la supuesta órbita de la tierra de muchos millones de millas como una línea de base. (...) Es inútil decir, en la explicación, que este desplazamiento inexistente, ya que se demostrará a partir de datos prácticos, en un capítulo posterior, que todas las luminarias en el firmamento están a sólo unos miles de millas de la superficie de la tierra.