por Alvaro Vary Ingweion Bayón
La posición del sol en el cielo demuestra que la tierra es esférica. Si quieres entender por qué, toma asiento y presta atención, porque te lo explicaré en las siguientes 1642 palabras
Pongámonos en situación. Solsticio de invierno, estamos en el (mal llamado) trópico de capricornio, en meridiano 20º Este, en algún punto entre Namibia y Botsuana. Son las 12:00 del mediodía hora solar, y el sol se encuentra a 90 grados sobre el horizonte.
En una tierra plana, el sol está sobre tu cabeza en su recorrido sobre el disco. Seis horas antes estaba sobre el trópico de capricornio también, pero a 90º al Este de tu posición, en el meridiano 110ºE, cerca de la costa occidental de Australia. Seis horas más tarde, a las 18:00 hora solar el sol se encontrará sobre el mismo trópico, pero en el meridiano 70ºW, cerca de Antofagasta, Chile. A medianoche, a las 00:00, se encontrará a 160W sobre el trópico de capricornio, en algún lugar sobre el Pacífico sur, cerca del archipiélago de Cook. Bien.
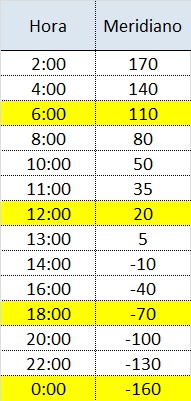
He decidido añadir a la ecuación varios puntos intermedios a intervalos meridianos de 30 grados (que equivalen a intervalos de 2 horas) para poder sacar suficientes puntos. Además, para mejorar la resolución, he incluido una hora antes y después del mediodía. Los meridianos se representan en positivo cuando son Este y negativos cuando son Oeste, para una fácil representación en la tabla. He marcado en amarillo los valores que os he puesto en el texto.
Sabiendo que la distancia entre el polo Norte y el ecuador es de aproximadamente 10.000 Km y que el trópico de capricornio está a 2.600 Km del ecuador, sabemos que el radio de la circunferencia que tiene nuestro trópico de capricornio en la tierra plana es de 12.600. Eso nos permite calcular distancias sin mayor problema.
¿Cómo calculamos esa distancia? Fácil. Primero calculamos el ángulo entre ambos puntos. Eso es sencillo porque hemos ido añadiendo los ángulos de 30º en 30º. Y ahora, sabiendo la distancia conocida entre cada punto y el centro (12.600), para los que están a 90º podemos aplicar el teorema de Pitágoras. Para los que están a 60º sabemos ya cuál es el resultado, pues forman triángulos equiláteros. Y para el que está a 180º solo tenemos que multiplicar el radio por 2. Para el resto, lo calculamos aplicado lo que se denomina teorema generalizado de Pitágoras. No te preocupes, ya te lo he calculado yo y lo puedes ver en esta tabla.
Ahora sigamos calculando. ¿Cuál es la altura aparente en grados a la que se encuentra el sol en cada una de esas horas? Supongamos, que es un suponer, que el sol en nuestra tierra plana da vueltas a una altura de 6 000 Km. Es un suponer, pero en realidad poco importa que lo haga a 3 000 o a 20 000. Solo cambiará la magnitud de lo que veremos, pero el aspecto de la gráfica será el mismo. Si la tierra es plana, el sol se encontraría a una altura que vendría determinada por un triángulo rectángulo en cuya base se encuentra la distancia calculada, y cuya altura sería la altura de 6 000 Km que antes hemos definido.
La tabla siguiente muestra el ángulo de altura del sol respecto al punto de observador, ese situado en el trópico de capricornio a 20ºE.
Una representación gráfica ayudará a arrojar un poco más de luz, aunque de entrada ya vemos alguna cosa un poco rara...
En efecto, pasa una cosa muy curiosa. Y es que vemos que el sol nunca llega a ponerse. Curioso, verdad? El sol, lo más bajo que llega a estar, es a 13 grados de inclinación sobre el horizonte.
Si hago los cálculos a partir de una tierra esférica, nos encontramos que el sol sigue encontrándose a 90º sobre nuestras cabezas a las 12:00, pero, usando solo la geometría (e ignorando la atmósfera adrede), la posición aparente del sol en función de la hora se convierte en una tabla muy curiosa (los números negativos, subrayados en gris, implican que el sol está más allá de la curvatura del horizonte, "al otro lado del mundo").
Al colocar estos nuevos datos en la gráfica nos encontramos con esto, donde el azul es el recorrido del sol en la tierra plana y el naranja es el recorrido del sol en la tierra esférica.
Ahora solo tendríamos que comprobar la posición del sol en el cielo en el mundo real, para saber si encaja con la predicción del modelo terraplanista o con la predicción del modelo esférico.
El mero hecho de que en las condiciones establecidas (recordemos, solsticio de invierno en el equinocio de capricornio) amanezca a las 6:00 hora solar y anochezca a las 18:00 hora solar, ya nos demuestra que el modelo de tierra esférica se ajusta mucho mejor a las observaciones que el modelo de la tierra plana, en el cual el sol ni siquiera llega a bajar por debajo de 13 grados sobre el horizonte. Pero aún queda algo más. Echar un vistazo a la realidad.
He utilizado un simulador para tomar los datos, pero un habitante de cualquier ciudad cercana al trópico de capricornio puede hacer las mediciones él mismo el próximo 22 de diciembre, y se dará cuenta de que, en efecto, son correctas.
Es evidente que a las 12 la gráfica está igual. Algo similar sucede en torno a las 7:40 y a las 16:20, puntos donde las gráficas se cruzan, pero, y al margen de durante la noche, hay cuatro rangos donde las diferencias son claras. Entre las 6:00 y las 7:00, entre las 8:00 y las 11:00, entre las 13:00 y las 16:00 y entre las 17:00 y las 18:00. Así que he decidido tomar esos cuatro rangos clave para observar la altura a la que se encuentra el sol en esos cuatro momentos. Podéis hacer eso mismo con el programa Stellarium (recordad colocar el 22 de diciembre y usar la hora solar; si tenéis dudas, colocaos en el meridiano 0 y usad UTC-0).
Los datos que he tomado corresponden con las 6:20 (primer rango), las 9:00, a las 10:00 (segundo rango), a las 12:00 (control), a las 14:00, las 15:00 (tercer rango) y las 17:40 (cuarto rango). Asimismo he comprobado la hora exacta de amanecer y anochecer de esa latitud y longitud, con el fin de que queden también patentes en la gráfica Esta es la tabla de datos reales.
Si incorporamos esos datos a la gráfica previa, encontramos un par de cosas interesantes. Veamos.
Lo primero que vemos es una clara correlación entre la gráfica que representa el movimiento real del sol (en verde) y la del modelo de la tierra esférica (en naranja), mientras que es muy distante de la gráfica que predice el modelo geocéntrico. Solo con eso, ya tenemos una primera conclusión clara: el movimiento aparente del sol sobre el cielo encaja con una tierra esférica y no con una tierra plana. Pero hay algo más.
Si bien vemos que en las horas centrales, entre las 10 y las 14 horas, las gráficas de la tierra real y la predicción de la tierra esférica encajan, cuando nos vamos a las horas cercanas al amanecer y al anochecer, las diferencias se ven acentuadas. Amanece antes de lo que el modelo predice, y anochece más tarde. ¿A qué se debe esto?
Esto sucede porque hemos ignorado la atmósfera en nuestro modelo. La atmósfera tiene un efecto de refracción que curva levemente la luz. Y mientras que en las horas centrales la cantidad de atmósfera que la luz ha de atravesar es mínima, durante la mañana y la tarde el sol está más bajo, tiene que atravesar más atmósfera y por tanto, esa refracción aumenta, haciéndose máxima en el mismo momento del amanecer y del anochecer.
Sea pues, queda patente que el movimiento aparente del sol en el cielo encaja con una tierra esférica y genera un conflicto ineludible e irresoluble con el modelo de tierra plana.
Me he tomado la molestia de calcular el ajuste estadístico para los pares de datos observados y esperados para una tierra plana y una tierra esférica ideal (recordemos que estamos ignorando factores como la atmósfera). Tenemos esta tabla de datos observados y esperados. He realizado una prueba de chi-cuadrada para cada conjunto de datos. Ese valor, que llamamos en estadística "valor P", nos indica cómo de parecidos o diferentes son los conjuntos que estamos comparando. El valor P es un estadístico que fluctúa entre 0 y 1; valores cercanos a 0 nos indican que existen diferencias significativas entre los conjuntos de datos escogidos, mientras que valores cercanos a 1 nos indican que los conjuntos de datos escogidos se parecen mucho. Dos conjuntos idénticos de datos dan un valor de 1.
En estadística, y de forma general, cualquier par de conjuntos que tengan un valor P inferior a 0.05 se considera que son significativamente distintos y por tanto, en esos casos, se rechaza la plausibilidad de la hipótesis. He cogido los datos centrales por mera comodidad para los cálculos.
Como se puede observar, existe un 98.9423 % de coincidencia entre los datos observados y el modelo predictivo de la tierra esférica. Una desviación de menos de un 1.1 % que sin duda es causada por la refracción atmosférica o a una toma de datos no lo suficientemente precisa.
Sin embargo, el modelo predictivo de la tierra plana tiene un asombroso 0.0002 % de coincidencia con lo que observamos en el mundo real. La desviación que encontramos entre los datos del predictivo terraplanista y los que observamos en la realidad es de un 99,9998 %. En este caso, con un valor P = 0.000002 RECHAZA de pleno la hipótesis de que la tierra sea plana. Sin embargo, un valor tan elevado de P = 0,989422 nos indica que la hipótesis de que la tierra sea esférica es perfectamente plausible
Pongámonos en situación. Solsticio de invierno, estamos en el (mal llamado) trópico de capricornio, en meridiano 20º Este, en algún punto entre Namibia y Botsuana. Son las 12:00 del mediodía hora solar, y el sol se encuentra a 90 grados sobre el horizonte.
En una tierra plana, el sol está sobre tu cabeza en su recorrido sobre el disco. Seis horas antes estaba sobre el trópico de capricornio también, pero a 90º al Este de tu posición, en el meridiano 110ºE, cerca de la costa occidental de Australia. Seis horas más tarde, a las 18:00 hora solar el sol se encontrará sobre el mismo trópico, pero en el meridiano 70ºW, cerca de Antofagasta, Chile. A medianoche, a las 00:00, se encontrará a 160W sobre el trópico de capricornio, en algún lugar sobre el Pacífico sur, cerca del archipiélago de Cook. Bien.
He decidido añadir a la ecuación varios puntos intermedios a intervalos meridianos de 30 grados (que equivalen a intervalos de 2 horas) para poder sacar suficientes puntos. Además, para mejorar la resolución, he incluido una hora antes y después del mediodía. Los meridianos se representan en positivo cuando son Este y negativos cuando son Oeste, para una fácil representación en la tabla. He marcado en amarillo los valores que os he puesto en el texto.
Sabiendo que la distancia entre el polo Norte y el ecuador es de aproximadamente 10.000 Km y que el trópico de capricornio está a 2.600 Km del ecuador, sabemos que el radio de la circunferencia que tiene nuestro trópico de capricornio en la tierra plana es de 12.600. Eso nos permite calcular distancias sin mayor problema.
¿Cómo calculamos esa distancia? Fácil. Primero calculamos el ángulo entre ambos puntos. Eso es sencillo porque hemos ido añadiendo los ángulos de 30º en 30º. Y ahora, sabiendo la distancia conocida entre cada punto y el centro (12.600), para los que están a 90º podemos aplicar el teorema de Pitágoras. Para los que están a 60º sabemos ya cuál es el resultado, pues forman triángulos equiláteros. Y para el que está a 180º solo tenemos que multiplicar el radio por 2. Para el resto, lo calculamos aplicado lo que se denomina teorema generalizado de Pitágoras. No te preocupes, ya te lo he calculado yo y lo puedes ver en esta tabla.
Ahora sigamos calculando. ¿Cuál es la altura aparente en grados a la que se encuentra el sol en cada una de esas horas? Supongamos, que es un suponer, que el sol en nuestra tierra plana da vueltas a una altura de 6 000 Km. Es un suponer, pero en realidad poco importa que lo haga a 3 000 o a 20 000. Solo cambiará la magnitud de lo que veremos, pero el aspecto de la gráfica será el mismo. Si la tierra es plana, el sol se encontraría a una altura que vendría determinada por un triángulo rectángulo en cuya base se encuentra la distancia calculada, y cuya altura sería la altura de 6 000 Km que antes hemos definido.
La tabla siguiente muestra el ángulo de altura del sol respecto al punto de observador, ese situado en el trópico de capricornio a 20ºE.
Una representación gráfica ayudará a arrojar un poco más de luz, aunque de entrada ya vemos alguna cosa un poco rara...
En efecto, pasa una cosa muy curiosa. Y es que vemos que el sol nunca llega a ponerse. Curioso, verdad? El sol, lo más bajo que llega a estar, es a 13 grados de inclinación sobre el horizonte.
Si hago los cálculos a partir de una tierra esférica, nos encontramos que el sol sigue encontrándose a 90º sobre nuestras cabezas a las 12:00, pero, usando solo la geometría (e ignorando la atmósfera adrede), la posición aparente del sol en función de la hora se convierte en una tabla muy curiosa (los números negativos, subrayados en gris, implican que el sol está más allá de la curvatura del horizonte, "al otro lado del mundo").
Al colocar estos nuevos datos en la gráfica nos encontramos con esto, donde el azul es el recorrido del sol en la tierra plana y el naranja es el recorrido del sol en la tierra esférica.
Ahora solo tendríamos que comprobar la posición del sol en el cielo en el mundo real, para saber si encaja con la predicción del modelo terraplanista o con la predicción del modelo esférico.
El mero hecho de que en las condiciones establecidas (recordemos, solsticio de invierno en el equinocio de capricornio) amanezca a las 6:00 hora solar y anochezca a las 18:00 hora solar, ya nos demuestra que el modelo de tierra esférica se ajusta mucho mejor a las observaciones que el modelo de la tierra plana, en el cual el sol ni siquiera llega a bajar por debajo de 13 grados sobre el horizonte. Pero aún queda algo más. Echar un vistazo a la realidad.
He utilizado un simulador para tomar los datos, pero un habitante de cualquier ciudad cercana al trópico de capricornio puede hacer las mediciones él mismo el próximo 22 de diciembre, y se dará cuenta de que, en efecto, son correctas.
Es evidente que a las 12 la gráfica está igual. Algo similar sucede en torno a las 7:40 y a las 16:20, puntos donde las gráficas se cruzan, pero, y al margen de durante la noche, hay cuatro rangos donde las diferencias son claras. Entre las 6:00 y las 7:00, entre las 8:00 y las 11:00, entre las 13:00 y las 16:00 y entre las 17:00 y las 18:00. Así que he decidido tomar esos cuatro rangos clave para observar la altura a la que se encuentra el sol en esos cuatro momentos. Podéis hacer eso mismo con el programa Stellarium (recordad colocar el 22 de diciembre y usar la hora solar; si tenéis dudas, colocaos en el meridiano 0 y usad UTC-0).
Los datos que he tomado corresponden con las 6:20 (primer rango), las 9:00, a las 10:00 (segundo rango), a las 12:00 (control), a las 14:00, las 15:00 (tercer rango) y las 17:40 (cuarto rango). Asimismo he comprobado la hora exacta de amanecer y anochecer de esa latitud y longitud, con el fin de que queden también patentes en la gráfica Esta es la tabla de datos reales.
Si incorporamos esos datos a la gráfica previa, encontramos un par de cosas interesantes. Veamos.
Lo primero que vemos es una clara correlación entre la gráfica que representa el movimiento real del sol (en verde) y la del modelo de la tierra esférica (en naranja), mientras que es muy distante de la gráfica que predice el modelo geocéntrico. Solo con eso, ya tenemos una primera conclusión clara: el movimiento aparente del sol sobre el cielo encaja con una tierra esférica y no con una tierra plana. Pero hay algo más.
Si bien vemos que en las horas centrales, entre las 10 y las 14 horas, las gráficas de la tierra real y la predicción de la tierra esférica encajan, cuando nos vamos a las horas cercanas al amanecer y al anochecer, las diferencias se ven acentuadas. Amanece antes de lo que el modelo predice, y anochece más tarde. ¿A qué se debe esto?
Esto sucede porque hemos ignorado la atmósfera en nuestro modelo. La atmósfera tiene un efecto de refracción que curva levemente la luz. Y mientras que en las horas centrales la cantidad de atmósfera que la luz ha de atravesar es mínima, durante la mañana y la tarde el sol está más bajo, tiene que atravesar más atmósfera y por tanto, esa refracción aumenta, haciéndose máxima en el mismo momento del amanecer y del anochecer.
Sea pues, queda patente que el movimiento aparente del sol en el cielo encaja con una tierra esférica y genera un conflicto ineludible e irresoluble con el modelo de tierra plana.
Me he tomado la molestia de calcular el ajuste estadístico para los pares de datos observados y esperados para una tierra plana y una tierra esférica ideal (recordemos que estamos ignorando factores como la atmósfera). Tenemos esta tabla de datos observados y esperados. He realizado una prueba de chi-cuadrada para cada conjunto de datos. Ese valor, que llamamos en estadística "valor P", nos indica cómo de parecidos o diferentes son los conjuntos que estamos comparando. El valor P es un estadístico que fluctúa entre 0 y 1; valores cercanos a 0 nos indican que existen diferencias significativas entre los conjuntos de datos escogidos, mientras que valores cercanos a 1 nos indican que los conjuntos de datos escogidos se parecen mucho. Dos conjuntos idénticos de datos dan un valor de 1.
En estadística, y de forma general, cualquier par de conjuntos que tengan un valor P inferior a 0.05 se considera que son significativamente distintos y por tanto, en esos casos, se rechaza la plausibilidad de la hipótesis. He cogido los datos centrales por mera comodidad para los cálculos.
Como se puede observar, existe un 98.9423 % de coincidencia entre los datos observados y el modelo predictivo de la tierra esférica. Una desviación de menos de un 1.1 % que sin duda es causada por la refracción atmosférica o a una toma de datos no lo suficientemente precisa.
Sin embargo, el modelo predictivo de la tierra plana tiene un asombroso 0.0002 % de coincidencia con lo que observamos en el mundo real. La desviación que encontramos entre los datos del predictivo terraplanista y los que observamos en la realidad es de un 99,9998 %. En este caso, con un valor P = 0.000002 RECHAZA de pleno la hipótesis de que la tierra sea plana. Sin embargo, un valor tan elevado de P = 0,989422 nos indica que la hipótesis de que la tierra sea esférica es perfectamente plausible










El modelo de la Tierra esférica está incorrectamente calculado, el eje terrestre está inclinado 23º27' (más o menos), de modo que aunque sea el solsticio de invierno (boreal), el Sol no sale por el este y se pone por el oeste:
ResponderBorrarhttps://www.suncalc.org/#/-23.4458,-0.0476,14/2017.12.21/11:58/1/0
de modo que aunque ciertamente esté a 90º sobre el horizonte a mediodía, al no salir por el este y ponerse por el oeste, el día dura más de 12h (en concreto según las cifras duraría casi 13.5 horas, por lo que el cálculo de la chi cuadrado debería rechazar la hipótesis de que el movimento real coincida con el simulado, que supone que el Sol sale por el este, se pone por el oeste, y recorre 15º por hora, empleando 12h en hacer el recorrido, porque hay demasiada diferencia entre una cosa y la otra.
Es solsticio boreal en el trópico. De todos modos, veo que tienes razón. Intentaré corregirlo cuanto antes.
BorrarLa chi-cuadrada encaja, porque el cambio que supone no genera diferencias significativas (las diferencias no son lo suficientemente altas como para que se note), sin embargo, y con toda probabilidad, si puedo hacer un día de estos el cálculo con el modelo correcto (y en ese caso, editaríamos el post con la corrección y un agradecimiento a tu aporte), la chi-cuadrada con los datos correctos saldrá aún más ajustada.
Saludos
Alvaro Vary Ingweion Bayón
Hola Álvaro:
BorrarDos cosas, en primer lugar no hace falta que hagas los cálculos, si me das una dirección de correo te los envío ya hechos.
En segundo lugar el tema de la chi cuadrado, yo creo que en este caso no procede, y te explico por qué, la chi cuadrado con n grados de libertad desde el punto de vista matemático es la suma de n variables aleatorias N(0,1) elevadas al cuadrado, y se emplea en casos en los que tenemos datos aleatorios que se deberían seguir esa distribución.
De los varios casos de uso, el más similar a lo que tenemos aquí es el de ajuste, que sirve para decidir si unos datos de "frecuencias" siguen una determinada distribución de probabilidad, y el valor que se ajusta a la chi cuadrado es la suma de las diferencias al cuadrado entre la frecuencia teórica y la observada, divididas por la frecuencia teórica, cada sumando es una N(0,1) al cuadrado, y la suma de los n sumandos debería ser entonces una chi cuadrado con n grados de libertad, y por eso se emplea esa distribución, y se acepta la hipótesis de que los datos aleatorios siguen la distribución teórica si quedan en la parte central (con el nivel de significación que se haya fijado previamente) de la distribución chi cuadrado y se rechaza si queda fuera, normalmente no se toma un intervalo simétrico, y la parte cercana al 0 queda como normal, aunque en realidad sea tan anormal como que el valor se dispare.
En el caso que nos ocupa, no tenemos frecuencias, tenemos una función del tiempo, la altura del Sol, y queremos comparar los valores experimentales con los teóricos, y los cocientes que hacemos para empezar dependen de las unidades empleadas, no da igual que midamos los ángulos en grados o en milisegundos, y en segundo lugar aparecen valores teóricos negativos de las 5:16:34 a las 6:00, lo que produce sumandos negativos, lo cual no tiene ningún sentido, todo lo que sumamos debe ser positivo si queremos que se ajuste a una distribución que sólo toma valores positivos como es una N(0,1) al cuadrado.
¿Qué es lo que se podría hacer aquí? pues simple, hacer medidas reales, con un margen de error, y aquí ya si que podrías contrastar la hipótesis de si los errores observados concuerdan con los teóricos, porque ya tendrías "frecuencias", agrupando los errores en intervalos. Naturalmente para eso deberíamos tener observaciones de verdad, como por ejemplo las del enlace siguiente:
http://gluonconleche.blogspot.com.es/2016/07/tierra-plana-o-globomundo.html
Supongamos por ejemplo que los errores de nuestras medidas siguen una N(0,1) con el ángulo medido en grados, y que hacemos medidas cada 10' de las 5:20 a las 18:40 lo que significa 81 medidas, supongamos que los errores los agrupamos por frecuencias de 1º, es decir redondeamos los errores al grado más próximo. De las 5:20 a las 6:00 hay 5 valores y otros tantos de las 18:00 a las 18:40, y en todos ellos el error es mayor que 9, habría que separarlos, pero vamos a suponer que todos son 9, y que por tanto la frecuencia observada del 9 sería 10. Para averiguar las frecuencias teóricas tendríamos que recurrir a las tablas de la normal, y el resultado es que debería haber 31 errores de 0, 20 de +1 o -1, 5 de +2 o -2 y cero del resto, por tanto la frecuencia teórica del 9 sería 0, con lo cual el sumando correspondiente al 9 sería (10-0)^2/0, que da directamente infinito. Por eso decía que la chi cuadado jamás podría dar por válida una curva teórica en la que el Sol sale por el horizonte a las 6:00, cuando en realidad sale a las 5:16:34, salvo si la precisión con la que mido los ángulos es pésima, y los errores pueden llegar fácilmente a los 10º.
Un saludo
PD: Como ya le he dicho a Alejandro en ocasiones anteriores, las gracias hay que dartelas a tí por el artículo.
transcribo respuesta de Álvaro:
Borrar"Está claro que el señor éste sabe más de estadística aplicada que yo. Dale las gracias y ofrecete para ampliar el artículo con una corrección hecha por él, yo estoy encantado de que me corrijan cuando lo hacen con conocimiento y con pruebas."
Por supuesto, el ofrecimiento me parece una excelente idea :) Creo que ya alguna vez antes de esto ya te lo había hecho...
Saludos
Sergio Alejandro Chifflet
PD: nuestro mail: refutandotp@gmail.com
Una pregunta: ¿la trayectoria del sol a lo largo del día terraplanista no debería ser una enorme elipse en el cielo que no corta el horizonte?
BorrarPorque yo jamás he visto eso...
Hola, los datos ya fueron corregidos Sergio?
ResponderBorrarNo. Álvaro todavía no ha tenido tiempo. Estarán pronto.
Borrar