¿Cuántas veces nos hemos encontrado con rutas aéreas que solo “tendrían sentido” en una Tierra plana?
El problema de las distancias y las rutas siempre se aborda desde un punto de vista incompleto, presentando casos puntuales en los que nunca se tienen en cuenta todas las variables. En ésta entrada lo analizaremos desde un punto de vista general, es decir, para cualquier caso posible y con las variables relevantes. Para eso haremos uso de una nueva herramienta del blog, pero primero, veamos algunos conceptos y explicaciones previos.
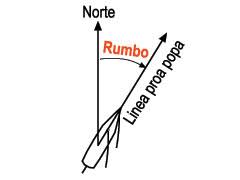
Rumbo
Por “rumbo” se entiende la dirección y el sentido por el que nos movemos en un camino, teniendo una referencia. Coloquialmente, cuando decimos “ponemos rumbo hacia tal lado” queremos decir que nos dirigimos hacia ese lugar. En navegación el rumbo suele expresarse como el ángulo en sentido horario con respecto al norte. Por ejemplo, si nos movemos al este, estamos siguiendo un rumbo de 90°. un camino sur-oeste tendrá rumbo 225°.
Mapas y rutas loxodrómicas
Los mapas son representaciones del territorio, con la particularidad de que hay una relación matemática entre lo que se representa y lo representado. No es solamente un dibujo sino que también tiene una métrica.
La elaboración de mapas en ese sentido tenían por supuesto un propósito: no solo tener una idea aproximada de la forma de ese territorio sino también conocer su extensión, la dirección precisa en la que se encontraba una localidad o la distancia entre poblados.
Históricamente, uno de los primeros mapas que se inventaron como tal, es decir, no sólo como un simple dibujo del territorio sino como una representación en la que había una correspondencia matemática, fueron las proyecciones cilíndricas. En éste tipo de proyecciones los meridianos y paralelos forman un entramado en el que las líneas son perpendiculares entre sí. Éste tipo de mapa era muy útil para viajar, ya que si se traza una línea entre una ubicación y un destino se puede ver que el rumbo es constante. La línea trazada corta los meridianos con el mismo ángulo, por lo que el camino tiene siempre la misma dirección con respecto a una referencia como una estrella particular o el norte que marca una brújula.

la ruta desde “A” a “B” corta los meridianos con el mismo ángulo
Durante siglos se navegó con ésta metodología a la que se llamó navegación loxodrómica (“loxo” viene del griego que significa “oblicuo”, por la línea representada en el mapa) creyendo que era la ruta óptima entre dos puntos, y ésto tenía una cierta lógica: si los mapas representan el mundo, y el camino más corto entre dos puntos de un plano es una recta, entonces una recta en un mapa representa el camino más corto.
Sin embargo se siguieron desarrollando distintos tipos de proyecciones cilíndricas ya que las rutas se aproximaban a una línea recta pero sin llegar a ser propiamente rectas, lo que se resolvió finalmente con los mapas de Mercator. Apenas unos años más tarde, el matemático portugués Pedro Nunes publica su “Tratado de la navegación” en el que hace notar que una línea loxodrómica no puede ser el camino más corto entre dos puntos de la Tierra. En particular, no se puede circunnavegar el globo siguiendo una loxodrómica: cuando se navega siguiendo un rumbo constante (distinto de perfectos 90° o 270°, este u oeste), la ruta se acerca en forma de espiral a uno de los dos polos y se queda dando infinitas vueltas sin llegar nunca a tocarlo.
Rutas ortodrómicas
En geometría se conoce como “geodésica” a la línea más corta que une dos puntos en una superficie dada. La aplicación inmediata del estudio de geodésicas es la navegación marítima o aérea en la que se recorren grandes distancias y se necesita optimizar recursos como tiempo y combustible.
El ejemplo más simple de una línea geodésica es la línea recta que une dos puntos en una superficie plana y que es el camino más corto posible. El camino más corto entre dos puntos en una superficie cilíndrica es un tipo de hélice. En una superficie esférica, todos los caminos entre dos puntos son arcos de circunferencia, pero el camino más corto será el arco de circunferencia de menor longitud, que coincide con el arco de un círculo máximo.
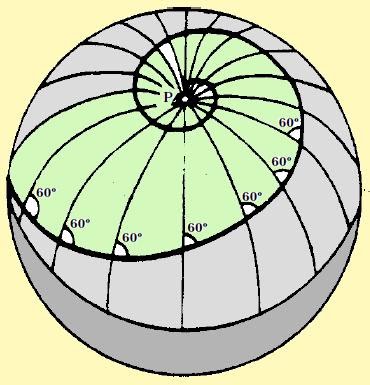
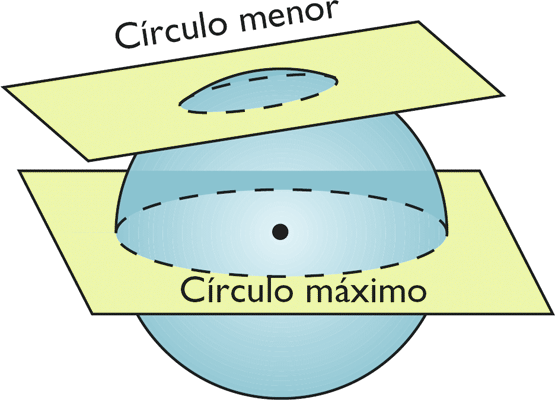
Un círculo máximo, también conocido como gran círculo, es la máxima circunferencia que se puede obtener de la intersección de un plano y una esfera, y eso ocurre cuando el plano pasa por el centro de la esfera. Una esfera tiene infinitos círculos máximos dependiendo de la orientación del plano, pero dados dos puntos en la superficie de la esfera, solo hay un solo círculo máximo que contenga a esos dos puntos y además el centro (tres puntos no alineados determinan un único plano).
Curiosidad: cuando los puntos en la esfera son antipodales (cuando son diametralmente opuestos) hay infinitas arcos de círculo máximo que los unen. Todos de 180° y todos con la misma longitud que será pi multiplicado por el radio de la esfera. En el planeta Tierra, lo máximo que nos podemos alejar desde donde estemos son unos 20000 km, justo en las antípodas.
En general, dada una superficie cualquiera, las matemáticas demuestran que la línea más corta que une dos puntos de esa superficie es la línea que tiene menor curvatura. Es por eso que coloquialmente se dice que el camino más corto en cualquier superficie es la línea “más recta”.
Resulta entonces natural que en una superficie esférica la línea geodésica siga un arco de círculo máximo, ya que de todas las circunferencias posibles, el círculo máximo es el de menor curvatura.
La ruta más corta entre dos puntos de la superficie terrestre se conoce como “ortodrómica”.
Una particularidad de las rutas ortodrómicas es que cambian el rumbo constantemente, algo que en la práctica es imposible de conseguir, caso contrario a lo que ocurre en una ruta loxodrómica en la que el rumbo es constante y es mucho más fácil de seguir. La diferencia de longitud entre una y otra es mínima, pero crece a medida que las distancias a recorrer son más grandes. Así que en la práctica, una solución efectiva es seguir una loxodrómica cuando las distancias son relativamente cortas ya que la economía es poca, y cuando las distancias son más largas, se traza una ortodrómica que se divide en muchos pequeños trayectos loxos, de ésta manera se va cambiando de rumbo cada cierto tiempo y el recorrido total se aproxima a una ruta ortodrómica. De ésta manera la navegación ortodrómica y loxodrómica siguieron (y siguen) coexistiendo a pesar de que la ruta óptima es la ortodrómica.
curva ortodrómica dividida en tres trayectos loxos.
Aún cuando hoy existen GPS, computadoras y sistemas automatizados, sigue siendo prácticamente imposible seguir una ruta ortodrómica perfecta, y ésto no solo porque sea una cuestión de ir cambiando de rumbo, sino porque las rutas dependen de otros factores como el clima, el tráfico, las derivas por vientos o corrientes marinas en el caso de la navegación marítima, o normas de seguridad como ETOPS que obligan a aviones a volar dentro del radio de un aeródromo. Así que en la práctica casi nunca se sigue una ruta ortodrómica perfecta, pero se trata de aproximar lo mejor posible.

Las normas ETOPS obligan a volar cerca de aeródromos

El vuelo real no siempre coincide con la ruta óptima.
Rutas “flatdrómicas”
Las rutas “flatdrómicas” no existen más que en el contexto de una supuesta Tierra plana: representa la ruta óptima en una supuesta Tierra plana. En una Tierra plana, la ruta entre dos puntos cualquiera debería ser una línea que se aproxime lo más posible a una recta. El cálculo de ese tipo de trayectoria es muy fácil ya que ocupa una simple trigonometría plana. En cambio las loxodrómicas y ortodrómicas (por recorrer una superficie esférica) se calculan con trigonometría esférica.
Asumiendo un valor cualquiera para el radio de lo que sería ese disco plano se puede también llegar muy fácil a la relación entre esas distancias y el tamaño de la “Tierra plana”, por lo que es posible establecer una matemática general que describa todas las posibles rutas para cualquier ubicación posible.
En la siguiente figura puede verse a simple vista lo que sería un vuelo entre Buenos Aires y Johannesburgo. Aún cuando no se han dado valores de distancias puede verse que el rumbo inicial del avión sería marcadamente noreste, de unos casi 30°. En la práctica el rumbo inicial es de unos 110° (sureste). Una diferencia enorme de 80° que resulta imposible de conciliar con la realidad.
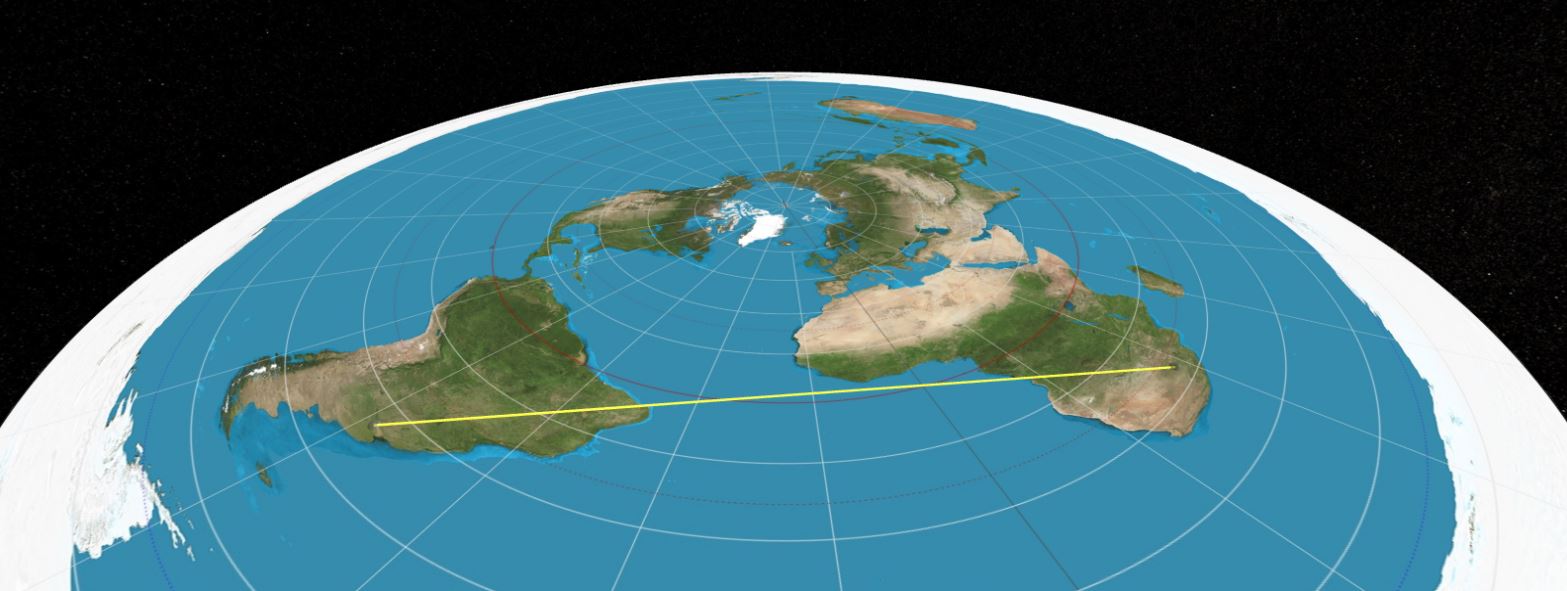
En una supuesta Tierra plana, la ruta entre Buenos Aires y Johannesburgo sería muy parecida a la línea amarilla.
La aplicación
La aplicación calcula rutas entre puntos dados mostrando las correspondientes trayectorias, distancias y rumbos. Las rutas calculadas se muestran sobre el globo terráqueo y también sobre un tipo de mapa circular que es una proyección acimutal equidistante polar, lo que sería el supuesto “mapa de la Tierra plana”.
Las rutas entre cada modelo (el globo terráqueo y el plano) se corresponden punto a punto, quiere decir, que las rutas atraviesan las mismas locaciones en los dos mapas.
Se muestran tres tipos de rutas:
Ortodrómica representada como una línea verde.
Loxodrómica representada como una línea roja.
“Flatdrómica” representada como una línea amarilla.
Lo que pretende la aplicación es mostrar la ruta óptima entre puntos en cada modelos y compararlos punto a punto con rutas de navegación reales, en términos de distancias y también de rumbos.
Vimos anteriormente que la ruta óptima en el globo terráqueo es la ortodrómica. Para el ejemplo clásico del vuelo directo Santiago de Chile - Sidney la ruta es de aproximadamente 11350 km, empieza con un rumbo inicial suroeste para bajar cerca del paralelo 60° sur para luego empezar a subir, completando el recorrido en unas 12 horas y media de vuelo a una velocidad promedio 900 km/h. Si proyectamos ese mismo recorrido en un plano de manera que pase por las mismas ubicaciones, la ruta sería de 39500 km y demoraría 44 horas. Incluso si el avión volara a 1062 km/h que es la velocidad del sonido a 11000 metros de altura, se demoraría 37 horas. Como dato para contrastar, el récord de vuelo comercial más largo sin escalas es Nueva York-Singapur que cubre unos 15400 km en unas 18,5 horas.
¿Qué pasaría en ese supuesto mundo plano si en vez de seguir la ruta hacia el sur que nos imponen las élites de la aviación comercial calculamos la ruta óptima? Ésta ruta óptima sería la “flatdrómica”, una línea recta entre Santiago de Chile y Sidney. No solo mediría 25700 km en total sino que seguiría un rumbo totalmente irreal hacia el noroeste, siguiendo la costa oeste de sudamérica, el golfo de Mexico y los Estados Unidos hasta alcanzar los 45° de latitud norte para luego llegar a Sidney desde el norte, durante un viaje de más de 28 horas y media. Incluso en ésta ruta óptima en el plano el viaje duraría más del doble.
La ruta óptima en la Tierra plana es obviamente la amarilla, que tendría unos 25700 km. La que se hace es la verde bordeando la Antártida. Esa línea verde que es claramente más larga mediría unos 39500 km, pero en la realidad solo mide 11330 km.
Contemplando otros casos
Por supuesto que éste es solo una caso puntual. Se podría pensar que las “Tierra plana” tiene en realidad un diámetro menor. Si ajustáramos el radio del disco del “mapa plano” a 6371 km la ruta de vuelo pasando por todas las ubicaciones por las que pasa en verdad mediría unos 12600 km, que si bien se acerca a lo que mide realmente. Desgraciadamente ajustar el tamaño del mapa para hacer encajar ese vuelo desencaja cualquier otra ruta que se pueda llegar a pensar, además de que ese ajuste dejaría unos 35,4 km por cada grado de latitud.
Se puede encontrar casos en los que a primera vista parecieran tener sentido en un mapa plano, como en el caso de los vuelos con escalas, pero si se analizan además de la forma de la trayectoria con los datos de rumbos y distancias vemos que no se acercan a lo que ocurre en verdad.
Incluso habrá casos en los que coincidan aproximadamente tanto en globo como en plano como en la realidad. Por ejemplo alguna ruta en el hemisferio norte en el que los mapas acimutales centrados en el polo norte no tienen distorsión. También alguna trayectorias norte-sur: en particular si trazamos una trayectoria cualquiera siguiendo un meridiano veremos que todas coinciden en distancia, rumbo y duración. Ésto es así porque en realidad el “mapa” de la Tierra plana es en realidad un mapa acimutal EQUIDISTANTE de una Tierra esférica en el que las líneas radiales que son los meridianos que equidistan justamente al centro de la proyección que es el polo norte.

Cualquier ruta norte-sur coincidirá tanto en el globo como en la “Tierra plana”, como por ejemplo Bariloche-Québec que comparten el mismo meridiano.
En conclusión: El único modelo en el que se pueden hacer coincidir TODAS las trayectorias tanto en distancia como en rumbo y las localidades que atraviesa es el modelo de Tierra esférica. NO EXISTE, ni se puede construir un mapa de una supuesta Tierra plana en el que se puedan hacer encajar todas las trayectorias, ni en distancias ni en duración ni en rumbo, tal como suceden en el mundo real. Ni siquiera variando el tamaño del mapa o la disposición de los continentes. El único modelo en el que sí encajan es en un globo terráqueo de 40000 km de circunferencia.
Pueden hacer la prueba ustedes mismos con la ruta que se les ocurra. Aquí el enlace a la app. También la pueden encontrar en la sección herramientas del blog.




















