Respecto del Experimento 7: Para 20 millas (32 km) el desnivel existente es de 14 metros. Dado que está viendo 32 Km con los ojos y en un primer vistazo, el ángulo de visión que tendríamos no sería más de 90º -un ángulo más amplio se desdibuja y perderíamos perspectiva-. Siendo así, la hipotenusa mide 32 Km, con lo que cada cateto (la distancia del ojo al barco) sería de 22,6 Km, y la altura de ese triángulo (esto es, la distancia hasta el punto de referencia) sería de 16 Km.
Para poder corresponderse con esos números, es necesario que la persona se sitúe al menos a 13,9 metros sobre el nivel del mar. Si por ejemplo nos mantenemos con los pies en la orilla y los ojos a 1,60 metros, nuestra distancia de horizonte óptico es de 5.502 metros, por lo que el máximo ángulo que podremos abarcar será de 11 Km aproximadamente.
En el primer caso, a 14 metros sobre el nivel del mar, viendo un total de 32 Km de horizonte, el arco que se forma tiene 14 metros de desnivel. Ver 14 metros de desnivel a 32 Km de distancia es como ver en una regla de 1 metro de longitud colocada horizontal a medio metro de distancia un desnivel de 0,43 milímetros.
En el segundo caso, estando con los pies en el mar y abarcando tan solo 11 Km de un solo vistazo, la elevación que se produce es de menos de dos metros, lo que equivale a ver en una regla de 1 metro de longitud colocada horizontal a medio metro de distancia un desnivel de 0,15 milímetros.
Si lo que esperamos es ver es un desnivel que sea claramente evidente, como el que dibujan en la representación -cuya relación entre longitud y altura es de 0,1, es decir, como ver un desnivel de 10 cm en una regla de 1 m- necesitaríamos ascender a un mínimo de 675 km de altitud, desde donde podremos observar un arco con una longitud de 6.747 Km. Esa es la distancia que necesitaríamos separar los barcos para que se pueda ver como muestra la Fig. 18
Por otra parte, usemos el sentido común... Si estamos parados en un lugar y el horizonte está a una distancia X, y tenemos un ángulo en nuestra línea visual entre el suelo sobre el que estamos parados y el horizonte, al cambiar la dirección en la que estamos mirando, el horizonte seguirá estando a la misma distancia, por lo que no habrá ninguna variación en el ángulo de nuestra línea visual. Podemos girar la vista 360º y el horizonte estará siempre a la misma distancia, y el ángulo será el mismo, por lo que el horizonte se nos aparecerá siempre como una línea recta. Para que la curvatura sea apreciable sin variar nuestro punto de mira, la altura desde la que efectuamos la observación debería ser de muchos kilómetros.
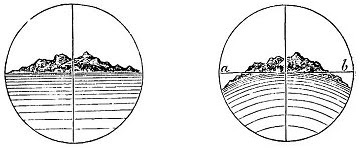
Sobre el Experimento 8, En primer lugar, para poder ver la isla de Wight en su totalidad de modo de poder realizar el experimento propuesto, deberíamos estar ubicados en un punto ubicado sobre la línea punteada, aproximadamente a la mitad de la isla y a una distancia tal que nos permitiera ver ambos extremos de ella. No hay manera de ver las 22 millas -es decir, 35 km- desde ningún punto de la otra orilla. Lo mejor que pude conseguir fueron solo 32 km, o 19.9 millas.
Aunque las condiciones de temperatura, presión y humedad sean las mismas en ambos puntos de la observación, si el aire tiene distintas densidades en las capas bajas que en las capas altas de la atmósfera habrá mayor o menor refracción atmosférica,
Sobre los faros citados por el autor, y pasando por alto que Dunkerke está sobre el Canal de la Mancha, en el norte de Francia, digamos que cuando se habla del alcance de la luz de un faro, no significa que un observador a 4 metros sobre el nivel del mar deba verlo. Se entiende que a esa distancia debería ser visible si el observador estuviera a la altura necesaria sobre el nivel del mar para poder verlo. Podríamos tener un faro excepcionalmente potente que tuviera un alcance de 100 kilómetros, pero solo sería visible para los aviones. Además, no olvidemos que por esta razón los barcos de principios del Siglo XIX tenían destinado un lugar para el vigía en el punto más alto disponible, en el tope de su palo mayor. Hay un problema en la interpretación que Rowbotham hace de los datos de los faros. Las menciones a los faros fueron tomadas por Eric Dubay y ya fueron considerados en el post correspondiente,que puede ser consultado aquí.
Anterior: Capítulo II: Experimentos 1 a 6
Por otra parte, usemos el sentido común... Si estamos parados en un lugar y el horizonte está a una distancia X, y tenemos un ángulo en nuestra línea visual entre el suelo sobre el que estamos parados y el horizonte, al cambiar la dirección en la que estamos mirando, el horizonte seguirá estando a la misma distancia, por lo que no habrá ninguna variación en el ángulo de nuestra línea visual. Podemos girar la vista 360º y el horizonte estará siempre a la misma distancia, y el ángulo será el mismo, por lo que el horizonte se nos aparecerá siempre como una línea recta. Para que la curvatura sea apreciable sin variar nuestro punto de mira, la altura desde la que efectuamos la observación debería ser de muchos kilómetros.
Sobre el Experimento 8, En primer lugar, para poder ver la isla de Wight en su totalidad de modo de poder realizar el experimento propuesto, deberíamos estar ubicados en un punto ubicado sobre la línea punteada, aproximadamente a la mitad de la isla y a una distancia tal que nos permitiera ver ambos extremos de ella. No hay manera de ver las 22 millas -es decir, 35 km- desde ningún punto de la otra orilla. Lo mejor que pude conseguir fueron solo 32 km, o 19.9 millas.
Sin embargo, eso no es lo importante. Rowbotham afirma que la observación se hace desde Spithead Head, Desde allí no es posible ver toda la costa de la isla, además de estar ubicado mucho más cerca de uno de sus extremos. En el mejor de los casos, solo podría ver unos 20 km de costa, equivalentes a sólo 12.4 millas.
Finalmente, las distancias hasta cada uno de los extremos visibles es muy diferente, por lo que no es posible que el la caída por curvatura sea igual en cada uno de los extremos
De todas maneras, como hemos visto en el tratamiento del Experimento 7, no es esperable una curvatura apreciable.
Finalmente, respecto del Experimento 9, digamos que no importa que el objeto esté sobre el agua, sobre el suelo o flotando en el aire, la refracción atmosférica se produce por diferencias de densidad en las distintas capas y/o zonas de la atmósfera. Es decir, no importa sobre qué tipo de suelo se encuentren el observador y el cuerpo observado sino de la cantidad y la naturaleza de la atmósfera que hay entre ambos objetos. El ejemplo sugerido por Rowbotham de la moneda en el cuenco con agua, no aplica aquí.
Aunque las condiciones de temperatura, presión y humedad sean las mismas en ambos puntos de la observación, si el aire tiene distintas densidades en las capas bajas que en las capas altas de la atmósfera habrá mayor o menor refracción atmosférica,
Sobre los faros citados por el autor, y pasando por alto que Dunkerke está sobre el Canal de la Mancha, en el norte de Francia, digamos que cuando se habla del alcance de la luz de un faro, no significa que un observador a 4 metros sobre el nivel del mar deba verlo. Se entiende que a esa distancia debería ser visible si el observador estuviera a la altura necesaria sobre el nivel del mar para poder verlo. Podríamos tener un faro excepcionalmente potente que tuviera un alcance de 100 kilómetros, pero solo sería visible para los aviones. Además, no olvidemos que por esta razón los barcos de principios del Siglo XIX tenían destinado un lugar para el vigía en el punto más alto disponible, en el tope de su palo mayor. Hay un problema en la interpretación que Rowbotham hace de los datos de los faros. Las menciones a los faros fueron tomadas por Eric Dubay y ya fueron considerados en el post correspondiente,que puede ser consultado aquí.
Anterior: Capítulo II: Experimentos 1 a 6
Siguiente: Capítulo II: Experimentos 10 y 11










No hay comentarios.:
Publicar un comentario
Comentarios soeces, insultos, amenazas, etc. Serán rechazados. Tienes libertad para publicar, pero no debes desperdiciarla.
Comentarios anónimos podrán ser publicados pero no serán respondidos.