Aceptando el desafío

En el post donde se refutaron las Pruebas 14 y 15 de Oliver Ibáñez, un usuario anónimo me dejó un comentario donde me desafió a refutar un video en el que, según él, se demostraba la inexistencia de la curvatura terrestre.

Aunque mi norma es no responder a comentarios anónimos, la curiosidad me llevó a ver el video en cuestión.

Primera parte - El muelle

Inicia en el minuto 1:55:29 anunciando que filmará al muelle Huntington desde la Península de Balboa, separados entre sí por 8.75 km.

En la mencionada filmación, puede apreciarse que el muelle no aparece oculto tras la línea del horizonte a pesar de la distancia:

Finalmente, hace una vista sin aplicar el zoom:

Cómo es esto posible?

Bien, en primer lugar, la caída tras el horizonte de seis metros solo se aplica si la altura del observador fuera cero:

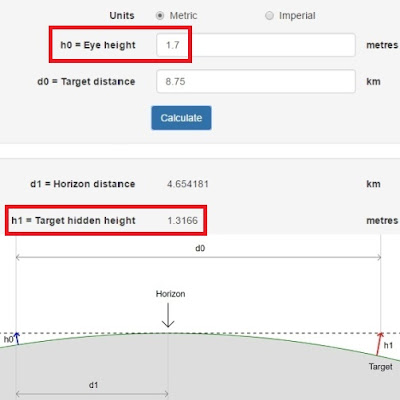
Sin embargo, si nuestro amigo tuviera una estatura más o menos normal y sus ojos estuvieran a 1,70 metros sobre el nivel del mar, las cosas cambian mucho:

Solo con estar parado sobre sus pies, los seis metros se convierten en apenas 1,32 metros, y eso sin considerar el pequeño oleaje que se aprecia. Puede el autor del video asegurarme que no falta algo más de un metro en la parte inferior de los pilares del muelle?

De todas maneras, la cosa no acaba allí. Resulta que el autor del video no está parado en la playa; puede verse a la derecha de la imagen, que está bastante más elevado que las personas que efectivamente lo están:

No estoy en condiciones de determinar la altura real pero entre la elevación del terreno y la altura del observador, una estimación muy conservadora podría ser de 4 metros. Ajustemos el cálculo con este valor:

Ahora resulta que la parte oculta tras el horizonte es de aproximadamente 20 centímetros. Menos que la altura de las pequeñas olas que pueden apreciarse en el video. En conclusión, es falso que no debieran verse 6 metros de la parte inferior del muelle. Apenas unos 20 centímetros, y eso ubicando al observador a solo cuatro metros de altura, aunque en la imagen parece ser bastante más. Así, la filmación presentada es perfectamente compatible con una tierra esférica.

Segunda parte - El velero
Inicia en el minuto 1:59:10 y por lo que hemos visto en la primera parte, a una altura del observador de 4 metros, la distancia hasta el horizonte es de 7,14 kilómetros (ver el último cálculo). Por lo que se aprecia en la imagen del final de esta parte (ver minuto 1:59:39) parece estar bastante por encima de unos seis metros sobre el nivel del mar, y considerando que no informa a qué distancia se encuentra la embarcación sino que estima, sin mayor fundamento que está como a 10 millas, podemos asumir que se encuentra a menos de 8 km y por lo tanto, tampoco hay nada en esta parte el video que no sea compatible con la tierra esférica.

Tercera parte - Las antenas
Inicia en el minuto 2:01:52 y nos muestra unas antenas ubicadas sobre una elevación del terreno a una distancia desconocida y  anuncia que no presentan ninguna inclinación.

Bien. Hacia dónde deberían estar inclinadas? Hacia la derecha? Hacia la izquierda? No. Deberían estar inclinadas HACIA ATRÁS. De acuerdo. Están inclinadas hacia atrás, pero ¿cuánto? es difícil saberlo, ya que ignoramos a qué distancia están esas torres. Sabemos que a 111.12 kilómetros estarían inclinadas hacia atrás un grado. Sin embargo, no parecen estar a mucho más de 11 km, Si así fuera, deberían estar inclinadas la décima parte de un grado, hacia atrás. Lógicamente, es imposible de apreciar.

Cuarta parte - Elly y Ellen

Inicia en el minuto 2:03:30 y nos muestra unas plataformas petroleras ubicadas a 19 km, diciendo que deberían estar ocultas por 27 metros de la curvatura terrestre. 

Como ya hemos visto, el autor de este video nunca toma en cuenta su propia elevación sobre el nivel del mar. Aparentemente, está haciendo sus tomas desde este lugar:

Aunque no puedo establecer su verdadera altura analizando la imagen, las personas en la playa me dicen que una estimación de seis metros sobre el nivel del mar es bastante conservadora, así que hagamos el cálculo con estos datos:

Ahora, veamos la imagen que ofrece como prueba. He colocado en la mitad inferior una línea amarilla que está aproximadamente a 8 metros de la superficie del mar. Comparen ahora ambas mitades, y verán que no es aventurado afirmar que, efectivamente, faltan los 8 metros inferiores en la fotografía superior:

Como ya se ha señalado, la inclinación HACIA ATRÁS es de aproximadamente la quinta parte de un grado, absolutamente imposible de apreciar. La parte oculta tras el horizonte se corresponde con lo que cabría esperarse en una tierra esférica. 

Todos los cálculos se han hecho sin tener en cuenta la refracción atmosférica por no ser necesarios, ya que aún sin tenerlos en consideración, y utilizando siempre alturas estimadas muy reducidas, los resultados obtenidos desmienten la afirmación de que este video demuestra la inexistencia de la curvatura terrestre.

Nada de lo expuesto en el video en cuestión se opone a la idea de una tierra esférica. De esta manera, creo haber satisfecho la solicitud de mi anónimo amigo terraplanista.

Actualización I

El visitante identificado como José, me ha dejado en la sección de comentarios un enlace que he visitado. Se trata de el lugar desde el cual se habría hecho el video. La altura estimada sería de unos 6 metros aproximadamente,

Actualización II

El video que se menciona originalmente en este post ha sido eliminado por su autor. Era un fragmento de un video mucho más largo conteniendo los fragmentos mencionados en aquél, por lo que este post ha sido editado haciendo referencia al video original.